Généralités

La propagation des ondes électromagnétiques dans le vide est en général différente de celle dans les lignes de transmissions d'une manière générale. On note que même s’il est difficile de déterminer le potentiel unique entre deux points sur une ligne dans le cas d'onde électromagnétique venant dans le temps, en mode TEM on peut le faire établir un effet dans les cas suivants:

De ces résultats découlent plusieurs applications utiles avec les grandes similitudes par rapport à la propagation en espace libre d'onde plane à savoir:

 

---

Ligne de transmission sans pertes

Transmission d'une onde T.E.M sur une ligne sans perte

TEM (E_z = H_z = 0) dans la direction de propagation. On rappelle que les formes intégrales des équations d'Ampère et Faraday sont:

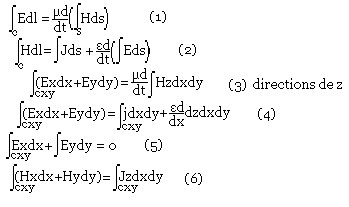
(5) et (6) sont les résultats obtenus pour le cas statique par conséquent on a deux conclusions:

Nous pouvons donc appliquer ces deux importants résultats à une ligne de transmission en déterminant le champ en n'importe quelle point en z dans la ligne le long de tous chemin entre les conducteurs au point d'ordonnée z.

De ce qui précède on peut considérer que le courant dans les deux conducteurs fait un champ magnétique en forme de spire faisant apparaitre l'inductance L à partir de laquelle on peut définir une inductance linéique.

De même on peut déduire des éléments capacitifs linéiques

Ces observations se justifient par le fait que le mode TEM satisfait aux conditions statiques impliquant une modélisation identique de cette ligne de transmission.

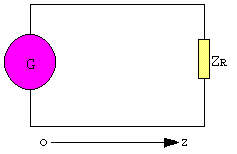
Soit une ligne de transmission de longueur l, alimentée à une extrémité par un générateur de tension haute fréquence et fermée à l'autre extrémité sur une impédance Z_R. En haute fréquence, la longueur l est plus grande devant la longueur d'onde.

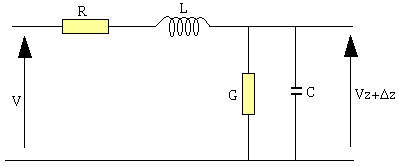
Pour faire l'étude de ces phénomènes, il convient d'adopter une modélisation de la ligne. Le model utilisé est un réseau qui comporte:

On peut s'attendre à ce que la variation du courant et de tension au long de la ligne ne doivent pas être discontinue. Pour anticiper cette notion, nous allons supposer que les différents éléments élémentaires de la ligne deviennent de plus en plus petits. Tout en s'assurant que la somme de ces éléments infinitésimal donne la longueur totale de la ligne. On va dont écrire les expressions de V et de I de la manière suivante:

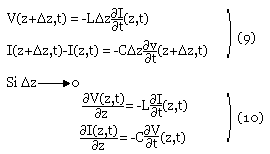
Les systèmes des équations (10) a plusieurs solutions. En dérivant (10a) par rapport à z et (10b) par rapport à t on retrouve le même système des équations différentielles de deuxième ordre relatif à la propagation des ondes électromagnétiques plane dans le vide.

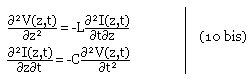
Si nous écrivons l'équation (10 bis) on obtient l'équation pour la tension.

Par le même raisonnement identique, on obtient l'équation pour le courant.

Dans ces équations on peut remarquer que le produit LC a la dimension de l'inverse d'une vitesse au carrée.

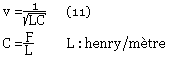
On peut démontrer que pour une ligne de transmission excitée par une onde TEM et émergé dans un milieu de caractéristique E et µ la relation suivante est respectée:

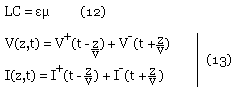
Comme dans les ondes planes V⁺ et I⁺ sont reliées par les relations suivantes:

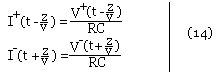
En tant donné que R_e = √(L/C) le système différentiel de 2^e ordre de la propagation de l'onde se résout dans les cas où une onde se propage dans une seule direction si Z_l = R_C = √(L/C)

L'impédance caractéristique

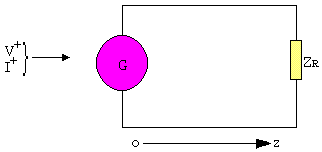
La discontinuité produite par Z_L est toute à fait semblable à la réflexion de l'onde sur un obstacle tel que décrite par l'électromagnétisme.
Nous traduisons cette discontinuité en différents coefficients de réflexion de la tension aux bornes de R_C.

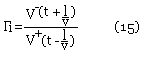
Si on remplace ce rapport au taux de réflexion aux expressions des courants et de tensions par l'équation (13)

La propagation d'une onde TEM présente donc l'analogie très important avec la propagation de l'onde électromagnétique plane en incidence normale d'une région d'indicez n₁, vers l'autre région avec indice n₂ et on aurait.

Nous allons maintenant nous intéresser aux valeurs des courants et tension, tout le long de la ligne.
Entre 0 < t < l/N sur la source, on a la seule tension et courant suivants:

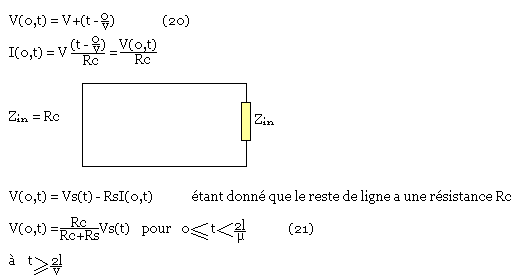
Au moment où le signal V_S(t) atteint la charge à t=l/µ est réfléchi vers la source, cette réflexion vers la source se fait suivant le diviseur de tension R_C/(R_C+R_S) et la même démarche utilisée précédente nous conduit à définir le coefficient de réflexion aux bornes de la source.

La coexistence de l'onde incidence (celle qui est réfléchie sur la charge) et celle de l'onde réfléchie (celle envoyé vers la source) comme une onde composite que sera régulée par le coefficient de réflexion aux bornes de la charge d'une part et le coefficient de réflexion aux bornes de la source d'autre part comme étant la source des courants et des tensions à ces instants comptes des coefficients r_s et r_L.