Page 3 sur 4
Ligne de transmission avec perte
Nous allons traiter maintenant le cas général d'une ligne avec pertes. Si nous sommes à un point z par rapport à l'origine et raisonnons sur l'élément compris entre z et z+ dz
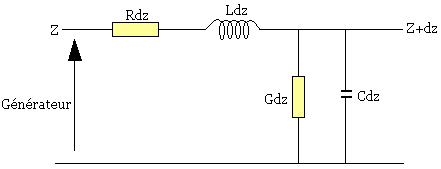
Soient v(z,t) et i(z,t) les valeurs complexes instantanées de la tension et du courant au point z. La variation de tension dv quant on se déplace de dz sur la ligne est égale à la somme:
- de la variation de tension -Rdzi due à la résistance
- de la variation de tension -Ldz due à l'inductance
Soit:
La variation d'intensité de courant di quand on se déplace de dz sur la ligne est égale à la somme:
- du courant s'écoulant par défaut d'isolement -Gdv
- du courant s'écoulant par la capacité -Cdz
Soit :
A partir de (1) et (2) on trouve facilement que i et v satisfaites les équations dites de télégraphistes.
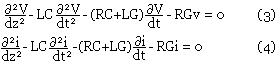
Si nous somme dans le régime sinusoïdal, alors les équations (1), (2), (3) et (4) deviennent:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale