Cas d'une excitation sinusoïdale sur une ligne sans perte (ω>>0)
Nous allons nous intéresser au cas où:
Nous allons supposer que les effets transitoires ce sont estompés: nous avons dont en notation complexe:
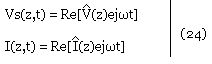
De l'équation (10) nous devront donc prouver que l'équation (25) est :
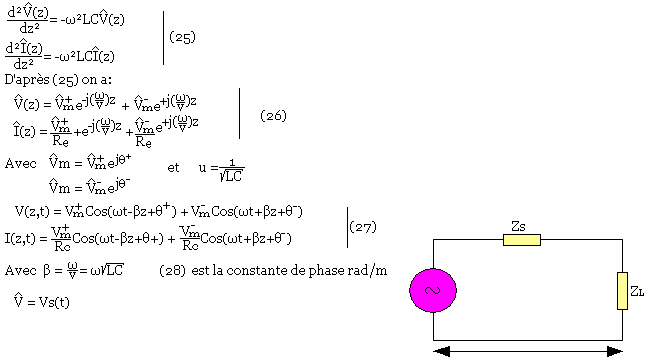
On peut définir le coefficient de réflexion complexe qui est:
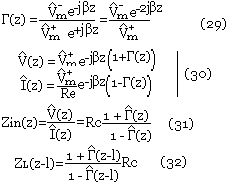
En pratique pour z = l on va avoir l'expression (31). On peut remarquer ici l'analogie entre l'onde plane en indice normale, et la propagation en mode guidé d'une onde
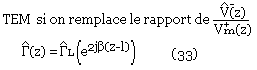
Le coefficient en tout point de la ligne peut être calculé en fonction de rL qu'est le coefficient de réflexion aux bornes de la charge, lequel peut être accordé par la relation:
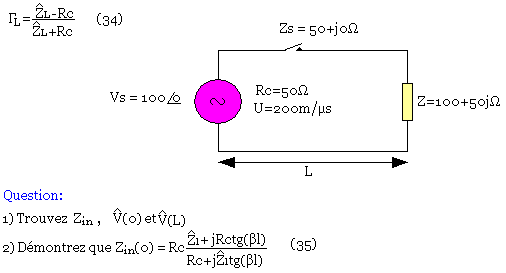
La relation (35) permet de déduire plusieurs résultats. D'abord de calculer l'impédance lorsque la ligne est court-circuitée.
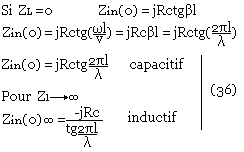
On peut tout de suite remarquer le comportement inductif ou capacitif de la ligne suivant que celui-ci estompe en ligne ouverte ou en court-circuit.
Il y a une relation d'une part entre Rc et Zin
Si on désigne par Xin les impédances d'entrée réactive, on obtient les diagrammes suivants en fonction de la longueur de la ligne.
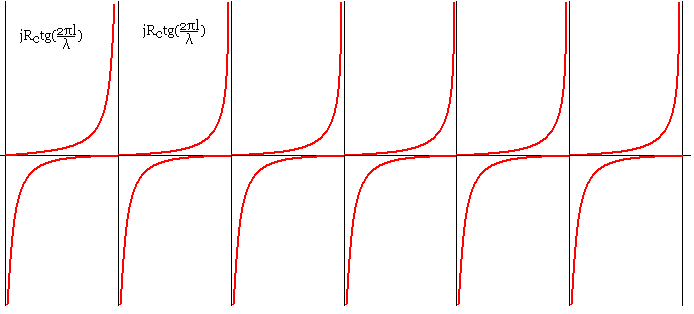
On peut également observer que l'impédance d'entrée se reproduit identiquement à elle même
Si nous prenons la valeur absolue de Id
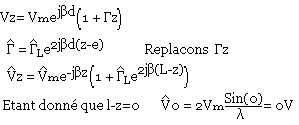
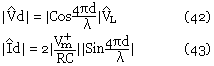
Si la ligne est chargée par ZL
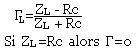
Dans le cas où Rc=ZL=0 la ligne est adaptée. Il n'y a pas de variation de courant ni de tension tout le long de la ligne.
Les expressions de Vd et Id exprimée en fonction de rL peuvent être représentée en fonction de d (distance) sur un diagramme de Grant en considérant la même vectorielle.
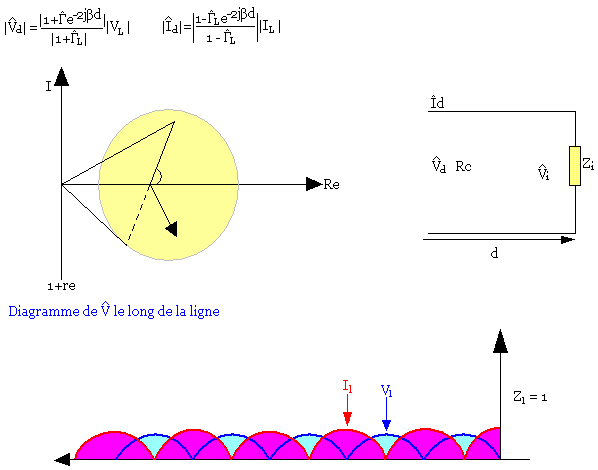
- Ligne ouverte: A un quart d'onde une ligne ouverte, le comportement de la tension sur la ligne est court-circuité.
- Court-circuit: Au quart d'onde d'une ligne en court-circuit le courant est nul et vd est différent de zéro.
- Ligne chargée l'impédance ZL quelconque.
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale