Les approximations dans les calculs des lignes de transmissions
Le cas des lignes à faibles pertes
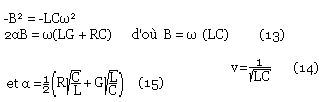
Notons que v est indépendant de la fréquence : un signal se propage donc sur la ligne sans distorsion.
D'après (12) et en négligeant RG, G2, on obtient:
De plus si les pertes dans le diélectrique sont négligeables par rapport aux pertes dans les conducteurs, on supprime dans (13) et (16) le terme en G1.
Minimisation des pertes
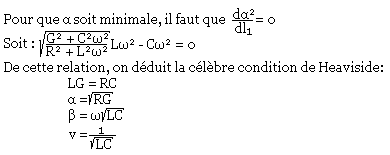
Expression de la tension du courant et de l'impédance
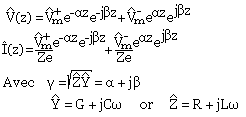
On note les similitudes entre les lignes sans perte. Il y a donc 3 remarques:
- Il y a apparition d'une atténuation sur la tension et le courant tout le long de la ligne
- L'introduction du facteur I/(LC) dans l'expression du courant introduit en déphasage de se dernier quand Z est complexe.
- L'expression de vitesse de propagation de l'onde dans le milieu v=ω/ß montre que cette vitesse est plus petite dans l'onde avec perte que celle d'une ligne sans pertes, car ß devient complexe et son module est plus grand que ßo=ω√(LC)
D'une manière générale, les résultats sur une ligne avec perte peuvent se déduire avec ceux d'une ligne sans perte en faisant quelques modifications:
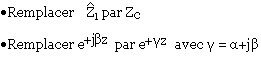
On doit cependant faire attention pour les autres expressions par exemple:
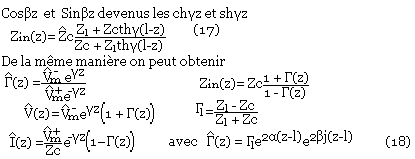
L'expression (18) fait apparaitre une nouvelle différence de comportement de la ligne avec pertes sur la ligne sans pertes. La puissance dissipée sur la ligne dans une portion de longueur d
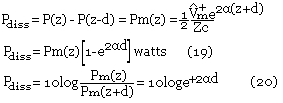
La constante peut être précisée en spécifiant les pertes pat unité de longueur sur une ligne adaptée. Si nous prenons l'expression de la propagation
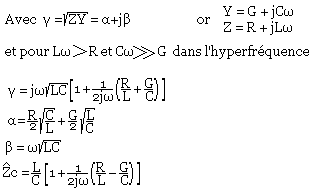
Les paramètres linéiques de la ligne
Nous avons vue que les paramètres linéiques Li et Ci pour une ligne sans pertes pouvaient être calculés comme ceux dans le cas d'une ligne statique à cause de la matière de l';ordre TEM calculé comme ceux dans le cas d'une ligne statique. Dans le cas de la ligne de transmission , si on élimine les effets de proximités des répartitions de charges sur les cylindres des conductions qui peuvent être négligés lorsque la distance entre les deux conducteurs est très grande par rapport aux sections. Les méthodes statiques permettent de déterminer les éléments des permittivités linéiques. On peut remarquer que le seul chargement noté dans l'équation de Maxwell est:
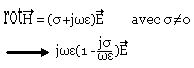
On peut dire que la seule différence avec une ligne avec perte si on considère la permittivité:
Dans le cas d'une ligne avec perte la capacité linéique est complexe et s'écrit:
Si on multiplie cette expression par jω et en comparant avec l'équation en-dessus on a:
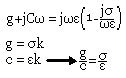
On peut s'apercevoir que:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale