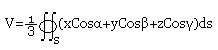- Cas de la courbe (C):
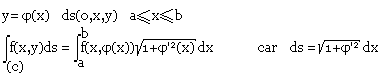
- Pour une courbe (C):
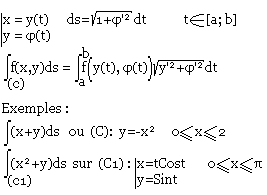
Intégrale curviligne de 2nde espèce
P et Q sont des fonctions à deux variables continues:
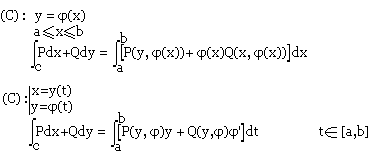
Quand on change le sens de parcours de la courbe (C) alors m'intégrale curviligne change de signe.
Exemple:
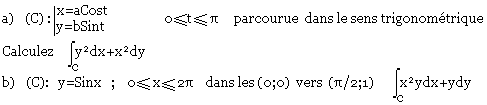
Cas d'une différentielle totale
On admet que l'on peut trouver U tel que
Exemple:
Déterminez U tel que dU = (4x+2y)dx + (2x-6y)dy et U(0;0) = 0.
Formule de Green pour le plan
(C) : courbe frontière du domaine plan (S), P et Q sont des fonctions continues avec dérivée partielle continue dans (S)+(C).
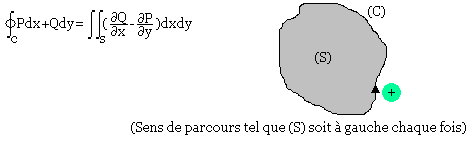
Application:
- Aire limité par le contour fermé (C) est:
- Travail ou circulation d'un vecteur.
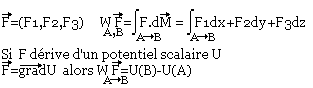
Exercice:
Intégrale de surface
Prenons la surface (S) z=φ(x, y).
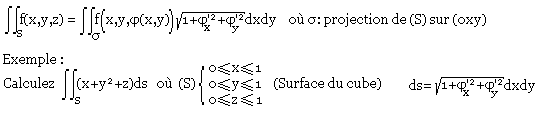
Intégrale de seconde espèce
(S) : surface
S+ : surface de S à plan tangent variant continument
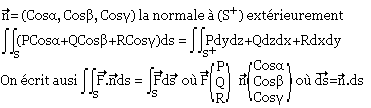
- Pour une surface donnée sous forme implicite:
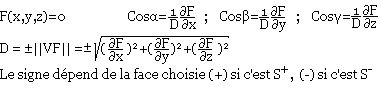
- Pour une surface donnée par:
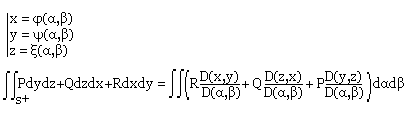
Exemple:
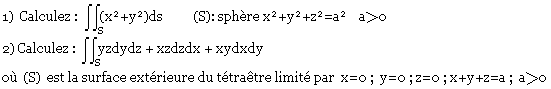
Formule de Stokes
(C) est un contour fermé limitant une fonction de surface (S) à deux faces contenues dans un domaine simplement connexe de l'espace.
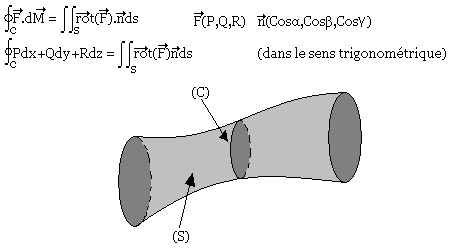
Exemple:
- Transformez par Stokes:
- Quelle est la condition sur P, Q et R pour que:
Formule d'Ostrogorski-Gauss
P, Q et R sont contenue avec leur dérivée partielle sur le domaine spatial V fermé, (S) est une surface fermé limitant le volume (V) fermé borné.
Propriété
Le volume d'un corps V limité par une surface (S) fermée est :
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale