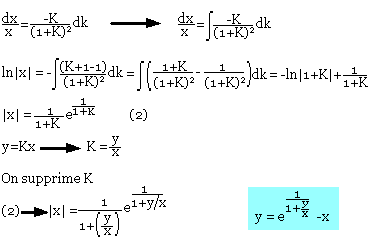Equation différentielle d'ordre 1
On rappelle qu'une équation différentielle est une relation de la forme R[f(n)(x),f(n-1)(x),...,f(x),x)]=0 (E), la résoudre consiste à trouver une ou plusieurs fonctions vérifiant (E) connaissant ou non une solution particulière de (E). Le plus haut degré de f(N) est l'ordre de l'équation différentielle.
Forme générale
Une équation différentielle d'ordre 1 est de la forme y'=f(x, y) (E) est solution de la forme y=G (x: constante).
Equations différentielles séparables
Forme générale y'=f(x)g(y) (E1) ou X0(x)Y0(y)dxX1(x)Y1(y)dy=0 (E2)
Résolution de (E2): On aura:
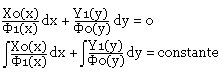
Exemple:
Trouvez la solution particulière de l'équation différentielle:
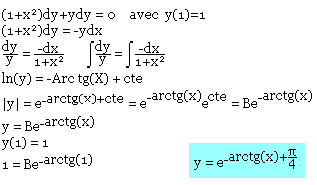
Equation différentielle homogène
Une fonction F(x, y) est homogène d'ordre N si:
![]()
Soit l'équation différentielle P(x,y)dx+Q(x,y)dy=0 où P et Q sont des fonctions homogènes d'ordre N. On amènera (E) sous la forme Y'=f(y/x) et on effectue Y=Kx
Exemple:
Trouvez la solution générale de (x22xy)dx+xydy=0 (E)
P(x,y)=x2+2xy , P(tx,ty)=t2x2+2t2xy=t2P(x,y)
Q(x,y)=xy ; Q(tx,ty)=(tx)(ty)=t2xy=t2P(x,y)
Posons y=Kx (où K et x sont des variables)
dy=Kdx+xdk
(E) : [x2+2x(kx)]dx+x(Kx)[Kdx+xdK]=0
[x2+2Kx2+K2x2]dx+Ks3dK=0
x2(1+2K+K2)dx+Kx3dK=0
(1+2K+K2)dx=-KxdK