Equation différentielle d'ordre 1
On rappelle qu'une équation différentielle est une relation de la forme R[f(n)(x),f(n-1)(x),...,f(x),x)]=0 (E), la résoudre consiste à trouver une ou plusieurs fonctions vérifiant (E) connaissant ou non une solution particulière de (E). Le plus haut degré de f(N) est l'ordre de l'équation différentielle.
Forme générale
Une équation différentielle d'ordre 1 est de la forme y'=f(x, y) (E) est solution de la forme y=G (x: constante).
Equations différentielles séparables
Forme générale y'=f(x)g(y) (E1) ou X0(x)Y0(y)dxX1(x)Y1(y)dy=0 (E2)
Résolution de (E2): On aura:
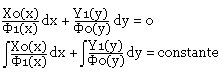
Exemple:
Trouvez la solution particulière de l'équation différentielle:
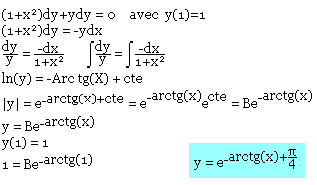
Equation différentielle homogène
Une fonction F(x, y) est homogène d'ordre N si:
![]()
Soit l'équation différentielle P(x,y)dx+Q(x,y)dy=0 où P et Q sont des fonctions homogènes d'ordre N. On amènera (E) sous la forme Y'=f(y/x) et on effectue Y=Kx
Exemple:
Trouvez la solution générale de (x22xy)dx+xydy=0 (E)
P(x,y)=x2+2xy , P(tx,ty)=t2x2+2t2xy=t2P(x,y)
Q(x,y)=xy ; Q(tx,ty)=(tx)(ty)=t2xy=t2P(x,y)
Posons y=Kx (où K et x sont des variables)
dy=Kdx+xdk
(E) : [x2+2x(kx)]dx+x(Kx)[Kdx+xdK]=0
[x2+2Kx2+K2x2]dx+Ks3dK=0
x2(1+2K+K2)dx+Kx3dK=0
(1+2K+K2)dx=-KxdK
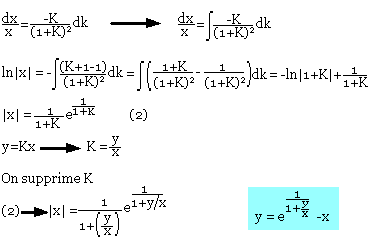
Equation différentielle linéaire
Une équation différentielle linéaire est une équation de la forme y'+a(x)y=c(x) (E)
On résout ce type d'équation en deux étapes.
1ereétape:
On pose c(x)=0 ; y'++a(x)y=0 (E')
(E') est l'équation homogène associée à (E).
22étape:
On utilise une solution particulière de (E'), laquelle est liée à une constante B, on résout alors (E) en considérant B comme une fonction B(x*
Exemple:
Résoudre xy'+2y=x3 (E)
xy'=2y=0
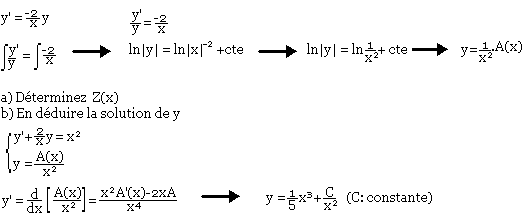
Exercice 1:
Résoudre l'équation homogène:
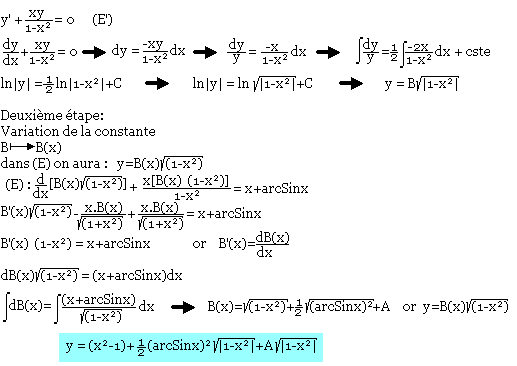
Exercice 2:
L'intensité I du courant électrique parcourant un circuit LR obéit à l'équation différentielle LdI/dt+RI=E où E est la f.e.m.
Calculez l'intensité I à l'instant après la mise sous tension (t=0) sachant que E=E0coswt et I=0 lorsque (t=0)
Résolution:
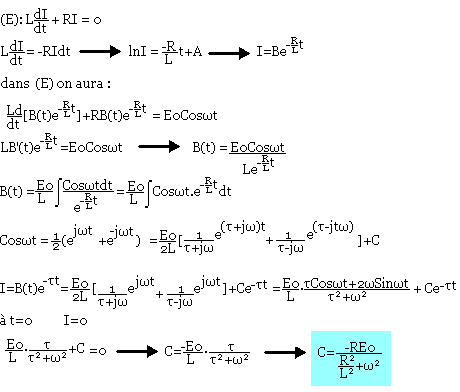
A chercher:
- y'+Sin(x+y)=sin(x-y)
- y'=ex+y+ex-y avec y(0)=0
- yy'=ln|y| avec y(2)=1
- xy'=xey/x+y avec y(1)=2
- xy'-y=x2cosx
- 4xy'+3y=-exx4y5
Equations différentielles d'ordre 2
Ce sont les équations différentielle de la forme (y",y',y,x)=0 donnant une solution générale R(y,x,c1,c2)=0 (ou de manière implicite y=f(x,c1,c2). Nous étudions 5 types d’équation différentielle.
1ertype: y"=f(y,y')
Dans ce cas il faut faire le changement de variable. En effet (1)
![]()
Exemple:
Résoudre les équations différentielles suivantes:
- 1+y'2 = yy"
- yy"-y'2 = 0
Rappel:
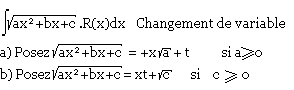
Autres types : quelques indications
- Type y=xy'+φ(y') faire y'=P
- Type F(x,y',y")=0 faire y'=ty
- Type F(y",x)=0 faire 2 intégrations de y"
Equation linéaire (II) à coefficient constant
Ce sont des équations différentielles de la forme a2y"+a1y'+a0y=f(x) (E) où a2, a1, a0 sont constantes, deux cas de solutions de ce type d'équation différentielle:
- 1e cas: aucune solution particulière connue
- 2e cas: o, connait une solution particulière
Si aucune solution particulière n’est connue.
1ièreétape: Résolution de l'équation différentielle homogène.
a2y"+a1y'+a0y=0 (E') on pose y=erx
(E'): a2r2erx+a1rerx+a0erx=0
ers(a2r2+a1r+a0)-0
Equation caractéristique (E,C)
Résolution de (E,C):
- Si (E,C) admet deux racines distinctes réelles:
α1 et α2 alors (E') a pour solution y=C1eαx+C2αx
- Si (E,C) admet une racine double, alors (E') a pour solution:
y = (C1+C2x)eαx
- Si (E, C) n'admet pas de solution réelle mais deux solutions
α1±βi complexe alors (E') a pour solution y=(C1Cosβx+C2Sinβx)eαx
Exemple:
Résoudre y"-4y'+13y=0
r2erx-4rerx+13erx=0
erx(r2-4r+13)=0
Solution:
y=e2x[c1sin3x+c2cos3x]
y=c1y1(x)+c2y2(x)
2eétape: Résolution de l'équation non homogène (E)
Supposons la solution de (E') de la forme c1y1(x)+c2y2(x), alors la variation des constantes se construit selon le système :
c1 ⟶ c1(x)
c2 ⟶ c2(x)
Et on résout le système:
c'1(x)y1(x)+c'2(x)y2(x)=0
[c'1(x)y'1(x)+c'2(x)y'2(x)=f(x)
Ce système nous permet de déterminer c1(x) et c2(x) et d'en déduire la valeur de la solution générale:
y=c1(x)y1(x)+c2(x)y2(x)
Exemple:
Résoudre y"-4y'+13y = 2x+1 (E)
Solution:
y=c1e2xsin(3x)+c2e2xcos3x
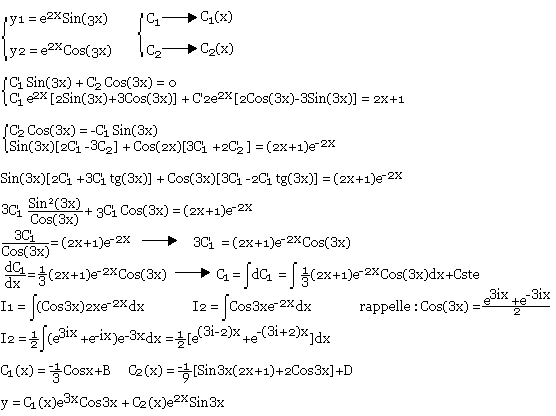
Equation différentielle linéaire à coefficient variable (2eordre)
Ce sont des équations de l'une ou l'autre des formes suivantes:
(E1) : a2x2y"+a1xy'+a0y=f1(x)
(E2) : (ax+b)2y"+(ax+b)1y'+a0y=f2(x)
Dans le cas (E1) on effectue le changement de variable (1) : x=et
Dans le cas (E2) ce sera (2) : ax+b=et
Relations remarquables
(1) : x=et avec t=ln(x) ; 1/x=e-t
Remarque:
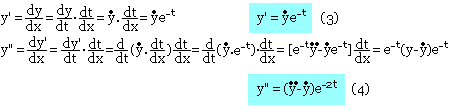
Exemple:
Résoudre x2y"-3xy'+4y=½x3
Problème:
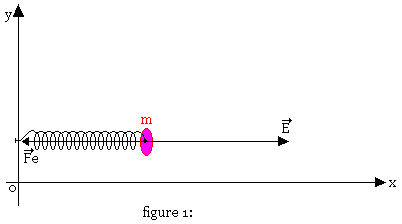
Soit à étudier les oscillations d'un point matériel de masse m soumis à l'action d'une force élastique Fe dont la grandeur est proportionnelle à l'écart x du point par rapport à sa position d'équilibre en présence d'une force perturbatrice
E0 = ESinγt
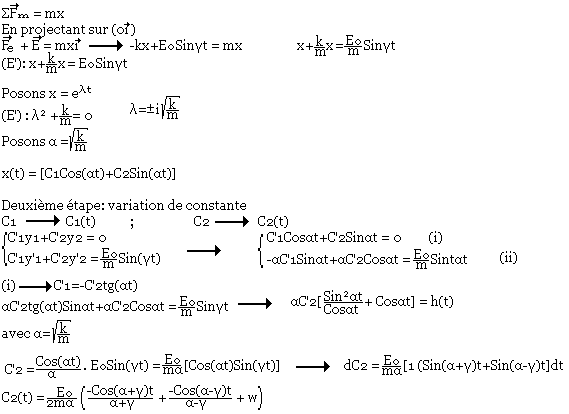
- Déterminez l'équation du mouvement de m (k>0)
- En déduire l'équation horaire de x(t)
A chercher:
- x2y"-xy'+y=0
- (4x+1)2y"-2(4x-1)y'+8y=0
- y"=x2+y avec y(0)=-2 et y'(0)=1
