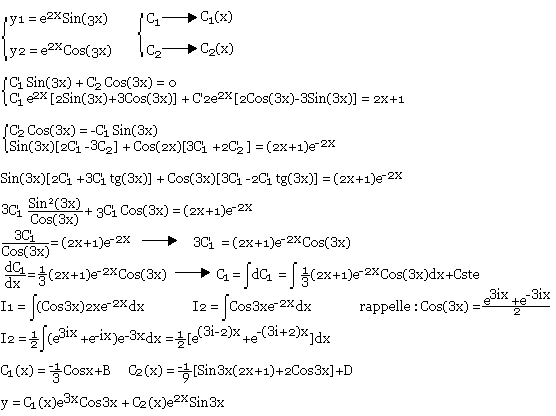Equations différentielles d'ordre 2

Ce sont les équations différentielle de la forme (y",y',y,x)=0 donnant une solution générale R(y,x,c₁,c₂)=0 (ou de manière implicite y=f(x,c₁,c₂). Nous étudions 5 types d’équation différentielle.

1^ertype: y"=f(y,y')

Dans ce cas il faut faire le changement de variable. En effet (1)

Exemple:

Résoudre les équations différentielles suivantes:

Rappel:

Autres types : quelques indications

Equation linéaire (II) à coefficient constant

Ce sont des équations différentielles de la forme a₂y"+a₁y'+a₀y=f(x) (E) où a₂, a₁, a₀ sont constantes, deux cas de solutions de ce type d'équation différentielle:

Si aucune solution particulière n’est connue.

1^ièreétape: Résolution de l'équation différentielle homogène.
a₂y"+a₁y'+a₀y=0 (E') on pose y=e^rx
(E'): a₂r²e^rx+a₁re^rx+a₀e^rx=0
e^rs(a₂r²+a₁r+a₀)-0
Equation caractéristique (E,C)

Résolution de (E,C):

α₁ et α₂ alors (E') a pour solution y=C₁e^αx+C₂^αx

y = (C₁+C₂x)e^αx

α₁±βi complexe alors (E') a pour solution y=(C₁Cosβx+C₂Sinβx)e^αx

Exemple:

Résoudre y"-4y'+13y=0
r²e^rx-4re^rx+13e^rx=0
e^rx(r²-4r+13)=0

Solution:

y=e^2x[c₁sin3x+c₂cos3x]
y=c₁y₁(x)+c₂y₂(x)
2^eétape: Résolution de l'équation non homogène (E)
Supposons la solution de (E') de la forme c₁y₁(x)+c₂y₂(x), alors la variation des constantes se construit selon le système :
c₁ ⟶ c₁(x)
c₂ ⟶ c₂(x)
Et on résout le système:
c'₁(x)y₁(x)+c'₂(x)y₂(x)=0
[c'₁(x)y'₁(x)+c'₂(x)y'₂(x)=f(x)
Ce système nous permet de déterminer c₁(x) et c₂(x) et d'en déduire la valeur de la solution générale:
y=c₁(x)y₁(x)+c₂(x)y₂(x)

Exemple:

Résoudre y"-4y'+13y = 2x+1 (E)

Solution:

y=c₁e^2xsin(3x)+c₂e^2xcos3x