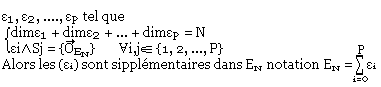Généralités
On définit deux structures d'ensemble: les "groupes" et les "corps".
Définitions
Quelques exemples d'espace vectoriel
- L'ensemble des matrices carrées d'ordres N est un espace vectoriel sur R (de dimension N2)
- L'ensemble des fonctions continues sur une intervalle [a, b] est élément vectoriel sur R.
- L'ensemble PN[x] des polynômes en x de degré inférieur ou égal à N est un élément vectoriel sur K de dimension (N+1)
Définition
Un sous espace vectoriel est lui-même un espace vectoriel.
Système de vecteurs
Soit F={e1,e2,...,eN} une famille de n vecteurs de E. L'objectif est de savoir s'il existe ou non un vecteur eg appartenant à F capable de s'écrire comme combinaison linéaire des autres vecteurs.
Si un tel vecteur existe, alors F est une famille liée (système indépendant)
Sinon , F est une famille libre (système indépendant)
Caractérisation des systèmes libres
La famille F={e1,e2,...,eN} est libre si et seulement si aucun vecteur de F ne peut s'écrire comme combinaison d'un autre.
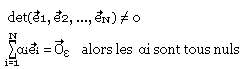
Caractère des systèmes liés
Exercice
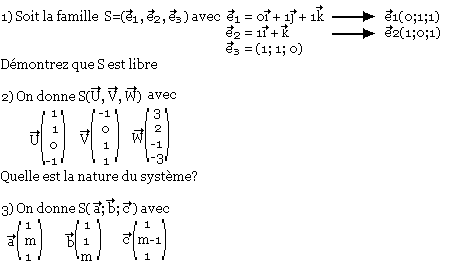
Pour quelles valeurs de m, le système est libre.
Correction:
Base et dimension d'un espace vectoriel
Système générateur
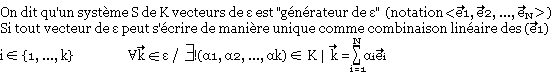
Base d'un espace vectoriel
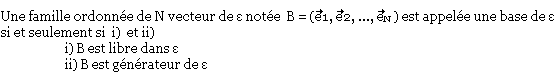
Dimension
Si ε admet une base de N vecteurs alors on l'appelle la dimension de ε (notée dimε)
Vocabulaire
Conséquence
Changement de base
Un espace vectoriel contient une infinité de bases.
Inversion de matrice:
Objectif: Effectuer des combinaisons linéaires pour obtenir I3 à gauche : M-1 apparaitra à droite.
Exercice:
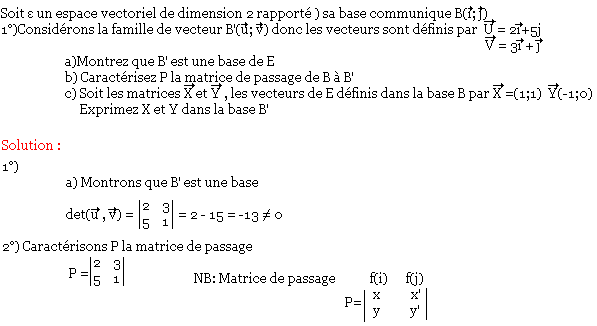
Matrice de passage
Conséquence:
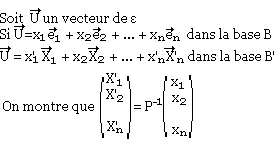
Somme directe de sous espace vectoriel
Soit EN un espace vectoriel de dimension N sur K, considérons A un sous espace vectoriel de EN alors:
0 ≤ dimA ≤ N (1)
Somme de sous-espace vectoriel
Si A et B sont deux sous ensembles vectoriels de EN avec dimA=K, dimB=r avec r+K=N (2).
Alors on notera EN=A+B (3)
Somme directe de sous ensemble vectoriel
Cas de deux sous ensembles vectoriels de EN
Cas de (P) sous ensemble vectoriel de EN
Soit P sous ensembles vectoriel de EN
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale