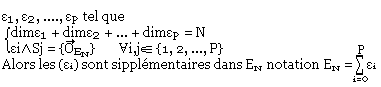---

Somme directe de sous espace vectoriel

Soit E_N un espace vectoriel de dimension N sur K, considérons A un sous espace vectoriel de E_N alors:

0 ≤ dimA ≤ N (1)

Somme de sous-espace vectoriel

Si A et B sont deux sous ensembles vectoriels de E_N avec dimA=K, dimB=r avec r+K=N (2).
Alors on notera E_N=A+B (3)

Somme directe de sous ensemble vectoriel

Cas de deux sous ensembles vectoriels de E_N

Cas de (P) sous ensemble vectoriel de E_N

Soit P sous ensembles vectoriel de E_N