La transmission du mouvement de rotation

Le mouvement de rotation peut être transmis d'un axe technologique à un autre axe technologique plus ou moins éloigné.
Les principales transmissions du mouvement de rotation sont:

Le système poulie-courroie permet de transmettre le mouvement de rotation d'un arbre moteur (axe technologique monté sur un moteur) à un autre arbre en le multipliant ou en le diminuant.

---

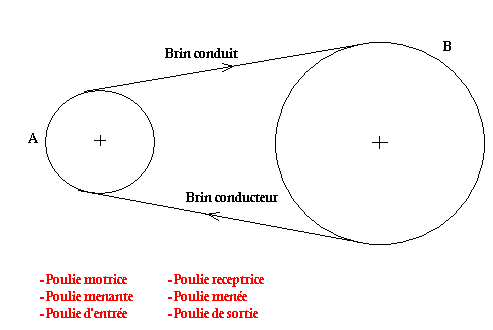
Principes

Brin conduit: c'est le brin qui sort de la poulie menante.
Brin conducteur: C'est le brin qui entre dans la poulie menante.

 

---

Observation

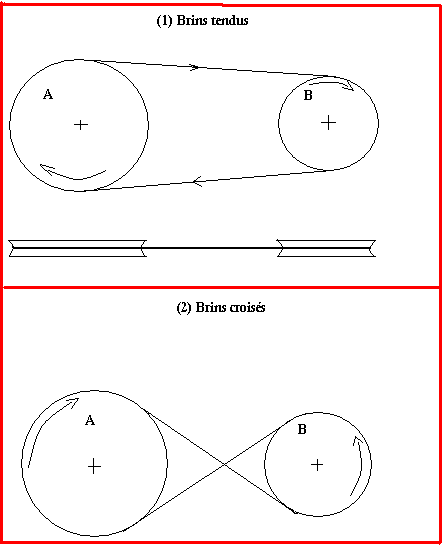
(1) Lorsque les brins sont tendus, les poulies A et B tournent dans le même sens.
Inconvénient: Lorsque les brins sont tendus il y'a mauvaise adhérence de la courroie sur les poulies.

(2) Lorsque les brins sont croisés les poulies A et B tournent dans le sens contraire.
Avantage: Lorsque les brins sont croisés, bonne adhérence de courroie sur les poulies.
Inconvénient: Usure de la courroie au niveau du croisement.

La transmission du mouvement par poulie-courroie est un mouvement réversible, c'est-à-dire si nous faisons tourner la roue A la roue B tourne et si nous faisons tourner la roue B la roue B, la roue A tourne.

 

---

Etude expérimentale

Les poulies de notre expérience ont respectivement pour diamètre D_A=20mm; D_B=40mm, où la poulie A est menante et la poulie B est menée.

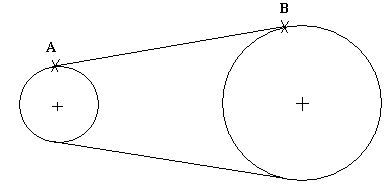
nA	1	2	3	4
nB	½	1	1,5	2
nB/nA	½/1	½	1,5/3=0,5	2/4=0,5

Si l'on note n_A le nombre de tour de la poulie menante A et n_B le nombre de tour de la poulie menée qu'effectue B. Etudions la relation n_B=f(n_A).

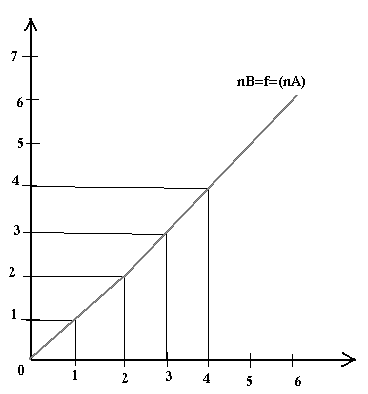
Etudions la représentation n_B=ƒ(n_A):
Nous constatons qu'il existe un rapport entre n_A et n_B. Ce rapport est appelé le rapport de transmission du système poulie-courroie et que l'on note K. Dans le cas de notre expérience K=n_B/n_A=0,5.
Le rapport de transmission du système poulie-courroie est égal au nombre de tours de la poulie menée sur le nombre de tour de la poulie menante.
K=(nombre de tours de la poulie menée)/(nombre de tours de la poulie menante)=n_B/n_A

 

---

Relation entre les diamètres

Les poulies de notre expérience avaient pour diamètre D_a=20; D_b=40. Faisons le rapport D_a/D_b=20/40=0,5=K.
Conclusion:
K=(Diamètre de la poulie menante)/(Diamètre de la poulie menée)=D_a/D_b
K=n_B/n_A=D_a/D_b

 

---

Relation entre les vitesses de rotation.

Rappel:

N=n/t, appliquons cette relation sur les poulies A et B. On a: N_A=nA/nB → nA=N_A.t
N_B=n_B/t → nB=N_B.t
K=n_B/n_A= N_B/N_A.
Le rapport de transmission K égal à la vitesse de rotation de la poulie menée sur la vitesse de rotation de la poulie menante.
K=(Vitesse de rotation de la poulie menée)/(Vitesse de rotation de la poulie menante).
Conclusion:
K=n_B/n_A=N_B/N_A=D_A/D_B.

 

---

Nature du mouvement

Si K>1, le mouvement est dit multiplicateur. Le diamètre de la roue menante est plus grand que le diamètre de la roue menée.
Si K<1, le mouvement est dit réducteur, le diamètre de la poulie menante est plus petite que le diamètre de la poulie menée.

 

---

Système de plusieurs courroies (le train)

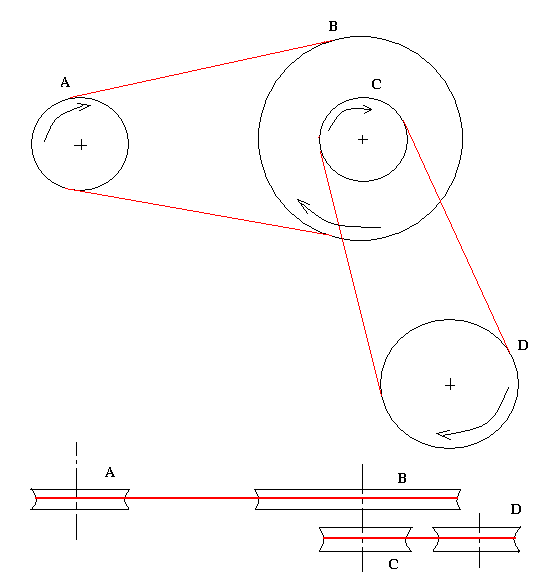
k₁=n_B/n_A=N_B/N_A=D_A/D_B;
k₂=n_D/n_C=N_D/N_C=D_C/D_D
K_G=K₁xK₂=nD/nA
K_G=K₁xK₂=N_D/N_A
K_G=K₁xK₂=(D_AxD_C)/(D_BxD_D).
Nous simplifions n_B et n_C d'une part, parce que les poulies B et C ont une même vitesse de rotation.
K_G=K₁xK₂=n_D/n_A=N_D/N_A=(D_AxD_C)/(D_BxD_D)

 

---

Le glissement

Les deux brins de la courroie (brins conduit et brins conducteurs) ne sont pas tendus de la même façon parce qu'il y'a un glissement au niveau de la poulie menée B. Ce glissement est de l'ordre x%.
Si n'_B désigne le nombre de tour que fait exactement la poulie menée B, n_B le nombre de tours que devrait faire la poulie menée B (sans glissement).
n'_B=n_B-(n_B.x)/100.

 

---

Exemple

Soit un système poulie-courroie le nombre de tour de la poulie menée est 30, le glissement est de l'ordre de 2%.
Calculez le nombre de tour (n'B) fait exactement par la roue menée B après le glissement.

AL:

n'B=nB-(nB.x)/100

AN:

n'B=30-(30x2)/100
n'B=29,4