Complément de mathématique
Les nombres complexes
Insuffisance de IR
Dans R on ne peut pas trouver la racine carrée d'un nombre négatif, il existe donc un ensemble plus grand que R appelé ensemble des nombres complexes noté C qui permet d'extraire des racines des nombres négatifs. j est appelé opérateur complexe.
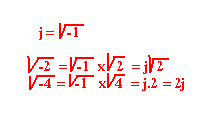
La propriété importante des nombres complexes:
- j2 = -1
- j3 = j2 x j = -j
- j4 = j2 x j2 = -1(-1) = 1
Définition des nombres complexes
Il existe 5 façons de représenter un nombre complexe mais on étudiera que 3 dans ce cours.
La forme algébrique
Quelque soit z appartenant à C; z=a+jb (a, b) appartient à R2.
- a: partie réelle
- b: partie imaginaire
La forme trigonométrique
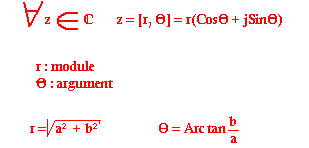
La forme polaire
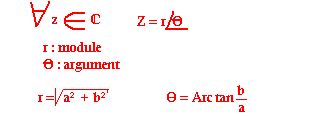
Quelques propriétés
Soient z et z' deux nombres complexes z=a+jb et z'=a'+jb'
- z = 0 si et seulement si a = b = 0
- z + z' = a + jb + a' + jb'
=a + a' + j(b + b')
= A + jB avec A = a+ a' et B = b + b' - z - z' = a + jb - (a' + jb')
= a - a' + j(b - b')
= A + jB avec A = a - a' et B = b - b' - z.z' = (a + jb)(a' + jb')
= aa' + jab' + ja'b + j2bb'
= aa' - bb' + j(ab' + a'b)
= A + jB avec A = aa' - bb' et B = ab' + a'b 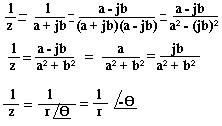
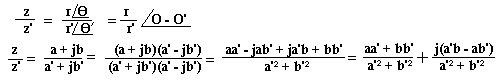
- z = z' ↔ a = a' et b = b'
Conjugué d'un nombre complexe
On appelle conjugué d'un nombre complexe de coordonnée a+jb le nombre complexe z' tel que:
![]()
Exemple
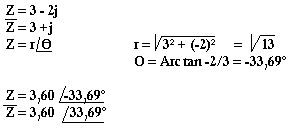
Propriétés
Soient Z = a +jb et Z' = a' + jb'
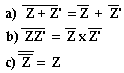
Quelques formules trigonométriques
Propriétés
- Cos(-x) = Cosx
Sin(-x) = Sinx - Cos2x + Sin2x = 1
- tgx = Sinx/Cosx cotgx = Cosx/Sinx
Formules de transformations
- Cos(a+b) = CosaCosb - SinaSinb
- Cos(a-b) = CosaCosb + SinaSinb
- Sin(a+b) = SinaCosb + SinbCosa
- Sin(a-b) = SinaCosb - SinbCosa
- tg(a+b) = (tga+tgb)/(1-tga.tgb)
- tg(a-b) = (tga-tgb)/(1+tga.tgb)
- Cosp + Cosq = 2Cos(p/2+q/2)Cos(p/2-q/2)
- Cosp - Cosq = -2sin(p/2 + q/2)Sin(p/2 - q/2)
- Sin + Sinq = 2Sin(p/2 + q/2)Cos(p/2-q/2)
- Sinp - sinq = 2sin(p/2-q/2)Cos(p/2+q/2)
Généralité sur le courant alternatif
On appelle grandeur alternative une grandeur qui est tantôt positive tantôt négative. Une sinusoïde est une grandeur alternative.
On appelle grandeur périodique une grandeur qui se repère identiquement à intervalle de temps régulier appelé période.
Soit X une fonction périodique
Soit t appartenant à R+, on a X(t+T)=X(t)
avec T: période en seconde
Exemple: Les fonctions cosinus et sinus sont périodiques de période 3x3,14
Quelques types de signaux
Signal carré
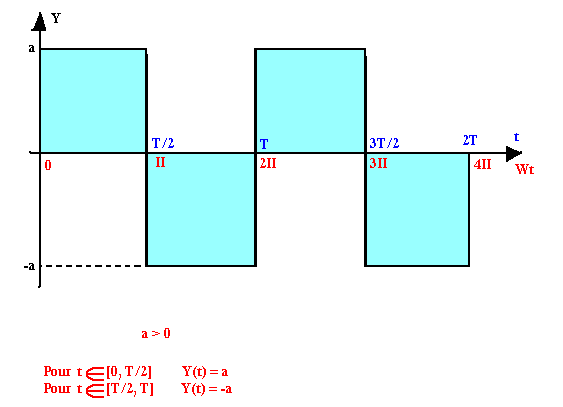
Signal à dent de scie
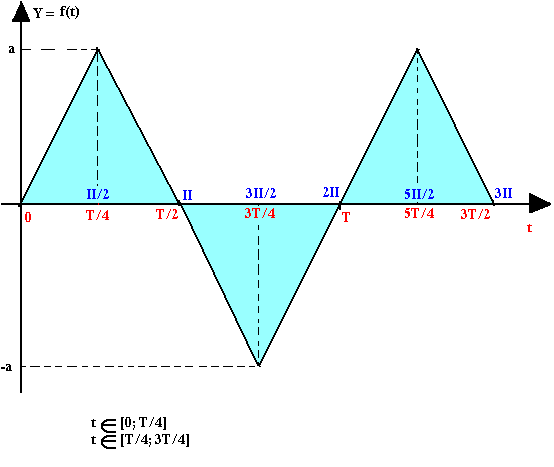
Signal sinusoïdal
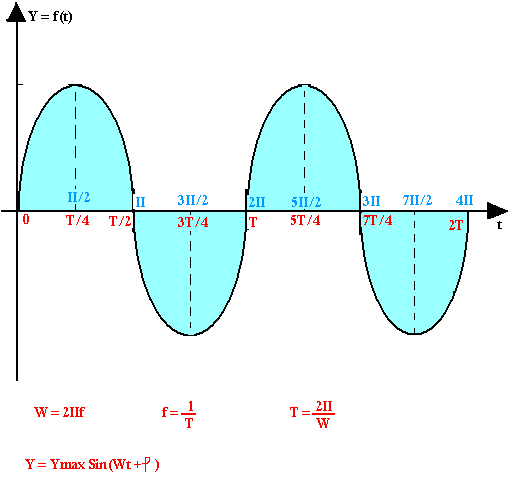
Dans la suite nous ne parlerons que des signaux alternatifs sinusoïdaux.
Valeur moyenne, valeur efficace
Valeur moyenne
La valeur moyenne Imoy = TAV d'un courant variable i=f(t) est égale à l'intensité I que doit avoir un courant continu constant pour transporter dans le même temps la même quantité d'électricité. Pour un courant alternatif sinusoïdal Imoy=0
La valeur efficace
La valeur efficace d'un courant variable i=f(t) est d'intensité I du courant continu constant qui produit le même dégagement de chaleur que i s'il passait pendant le même intervalle de temps dans la même résistance. Pour un courant alternatif sinusoïdal:
![]()
Représentations des grandeurs sinusoïdales
Représentation vectorielle
Soit un signal sinusoïdal U(t)=UmaxSin(wt+Þ), on lui associe un vecteur de module OM et d'angle Þ.
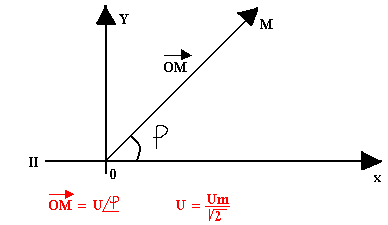
Représentation complexe
Soit U(t) une fonction sinusoïdale U(t)=UmSin(wt+Þ) la représentation complexe de U(t) est la suivante:
![]()
Elle correspond à la représentation polaire d'un nombre complexe où fait souvent abstraction de wt car les grandeurs électrotechniques ont souvent la même pulsation.
Représentation temporelle: Notation de déphasage
Ces signaux ne passent par zéro au même moment, on dit qu'ils sont déphasés
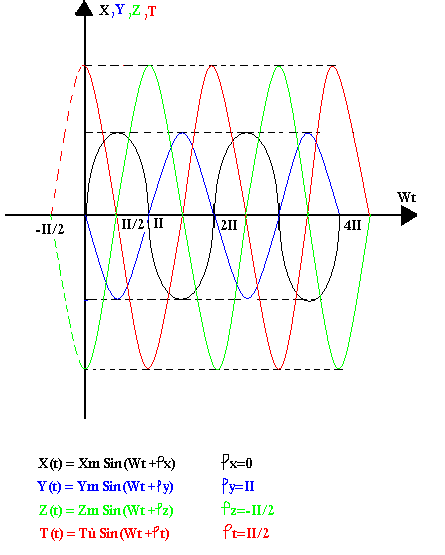
Relation tension courant dans les circuits R.L.C
Notion d'impédance
Notion de déphasage:
- DÞxy=|Þx-Þy|
- Si Þx-Þy>0; x est en avance sur y ou y est en retard sur x
- Si Þx-Þy<0; x est en retard sur y ou y est en avance sur x
- Si Þx-Þy=0; On dit que x et y sont en phase
- Si Þx-Þy=180° x et y sont en opposition de phase
- Si Þx-Þy=90°; x est en quadrature de d'avance sur y
- Si Þx-Þy=-90°; x est en quadrature de retard sur y
Notion d'impédance
Soit Z un nombre complexe, la loi d'ohm aux bornes d'un dipôle passif R.L.C est donnée par la relation suivante U=Z.I.
Z est l'angle de déphasage entre la tension U et le courant.
L'admittance Y est l'inverse de l'impédance T=1/Z, Y en siemens (s)
Cas d'une résistance
Exemple 1
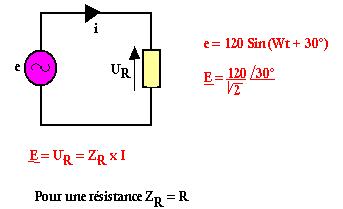
Dans une résistance le courant et la tension sont en phase.
Exemple 2
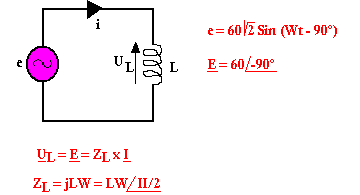
Ici la conclusion est simple, le déphasage entre les deux est de 90° et ici le courant est en retard sur la tension de 90°. Pour une inductance le courant est en retard sur la tension de 90°
Diagramme vectoriel
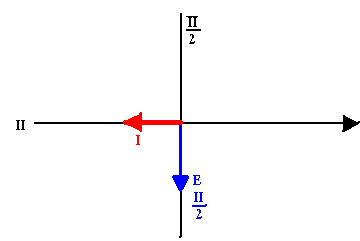
Cas d'un conducteur
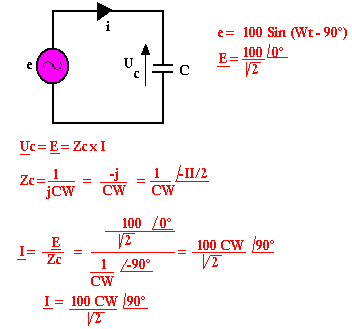
Le courant est en avance sur la tension de 90°
Diagramme vectoriel
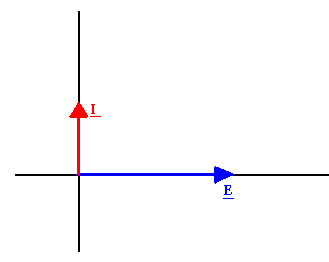
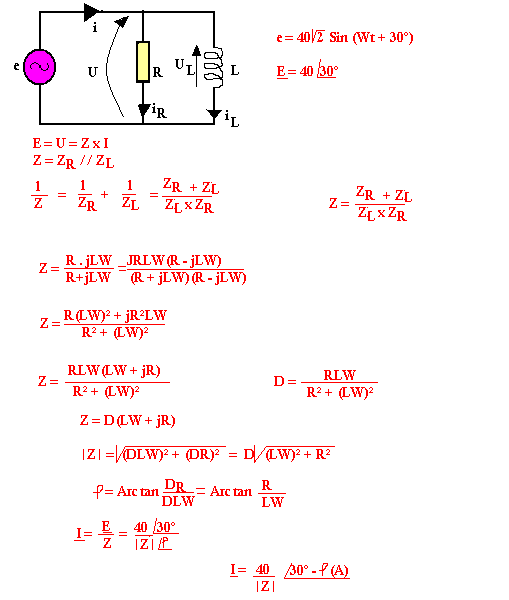
Cas d'une résistance et inductance
En série
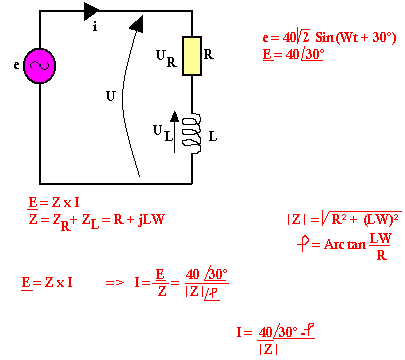
Par la maille
E - UL - UR = 0
E - ZL.I - ZR.I = 0
E = I(ZL + ZR)
E = I.Z
Diagramme vectoriel
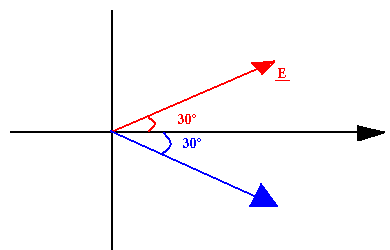
En parallèle
Puissance instantanée
On appelle puissance instantanée le produit de la tension et du courant instantané.
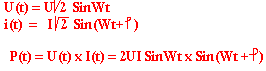
La puissance moyenne
La puissance moyenne est la moyenne de la puissance instantanée. Pour une sinusoïde on a:
P = U.ICosÞ
La puissance apparente complexe
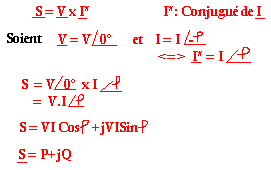
Avec:
- P = U.I.CosÞ (en Watt) puissance moyenne.
- Q = U.I.SinÞ (en VAR) puissance réactive
- S: puissance apparente complexe (en V.A)
![]()
Le triangle de puissance
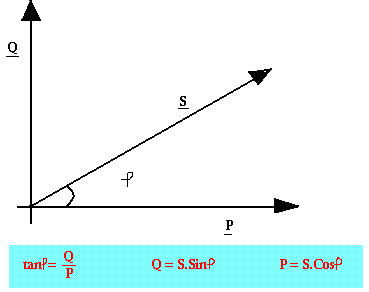
Le facteur de puissance
On appelle facteur de puissance noté FP, le rapport de la puissance moyenne sur la puissance apparente. Pour une sinusoïde, on a: FP=P/S=V.IcosÞ/V.I=CosÞ
↔ FP = CosÞ
Application au circuit R.L.C
Résistance
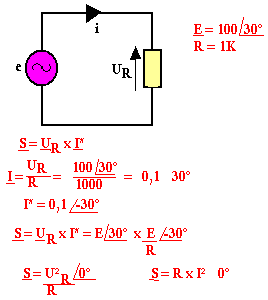
La résistance ne consomme que la puissance active.
Inductance
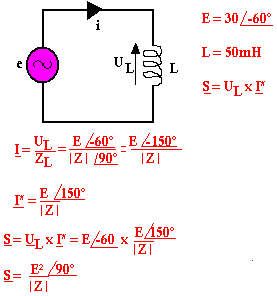
Le condensateur
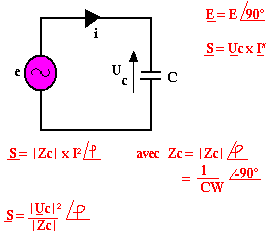
Compensation du facteur de puissance
Dans certaines applications de l'électronique, le facteur de puissance (CosÞ) est souvent trop petit et on a besoin de le ramener au tour de 1.
Comme le cosinus Þ est généralement arrière (circuit inductif), l'artifice consiste à mettre en parallèle avec le réseau un condensateur qui va annuler l'action Q existant.
Exercice:
V = 220V - 50Hz
P = 10KW
CosÞ = 0,66ARR
Calcul c pour CosÞ=0,93
Qinst = P.tgÞ avant la comparaison
Q'inst = P.tgÞ' = Qinst + Qc
CosÞ = 0,66 ↔ Þ = 48,7°
CosÞ' = 0,93° ↔ Þ' = 21,56°
Q'inst = P.tgÞ - V2.C.ω = P.tgÞ' ↔ P.tgÞ - P.tgÞ' = V2.C.ω
AL:
C = P(tgÞ-tgÞ')/V2ω
AN:
C = 10x103(1,13-0,39)/2202x314 = 4,8x10-
Etude de la résonance
Un dipôle est à la résonance si l'impédance de ce dipôle ou de ce circuit est purement résistif pour une fréquence f0 donnée appelée fréquence de résonance.
Soit Z cette impédance Z=a+jb
b=0 ; |Z|=a ; Þ=0° ou 180°
Etude des circuits RLC séries
Fréquence de résonance (f0)
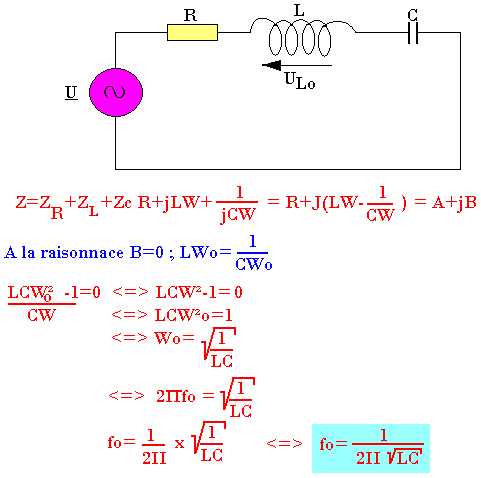
Quelques définitions
On appelle cœfficient de qualité Q le rapport entre la valeur maximale de l'énergie stockée par l'énergie dissipée par période.
Q = 2x3,14QS/QD
QS = ½LI2max = ½CV2max
QD = R(Imax/2½)2/f0
Pour les circuits en séries, le facteur de qualité Q est aussi le facteur de surtension pour les bobines. On a alors Q=ULo/U
ULo est la tension aux bornes de l'inductance à la fréquence de résonance. On a donc:
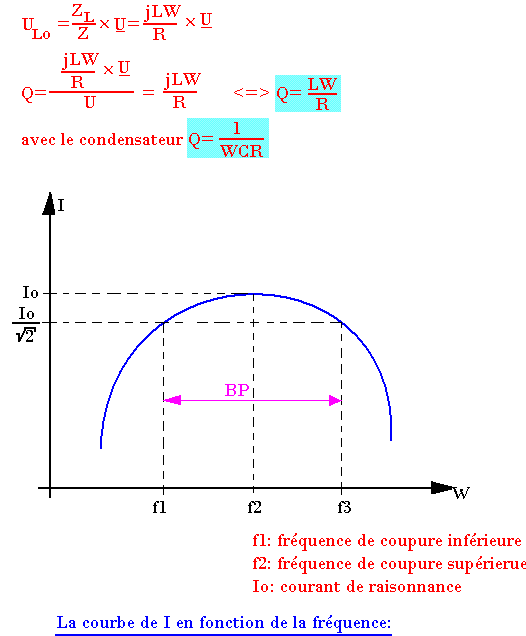
f1 et f2 sont définis pour I=I0/2½ c'est-à-dire à la moitié de la puissance active fournie bau réseau quand la fréquence est f0.
On montre que:
Q = ω0/(ω2-ω1) = f0/(f2-f1) = f0/BP avec BP:Bande passante
BP = f2 - f1
W0 = (ω1.ω2)½
f0 = (f1.f2)½
Etude d'un circuit parallèle
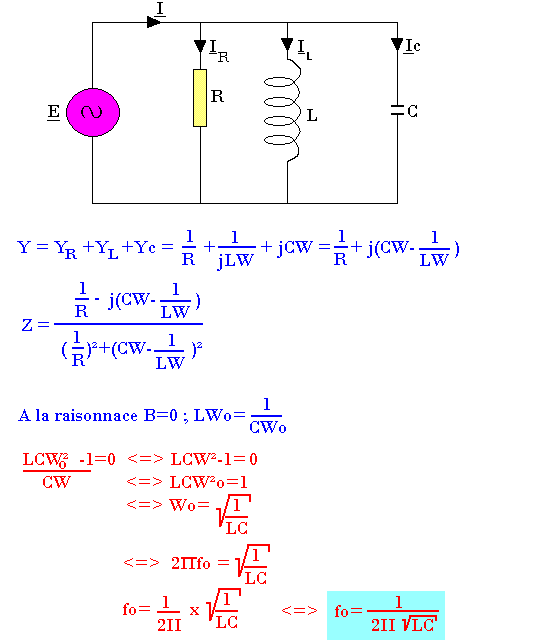
Le cœfficient de qualité Q est égale au cœfficient de surintensité du condensateur.
Q=ICo/Io
ICo = YCoI/Yo = jCωI/YR
ICo/Io = jCωR
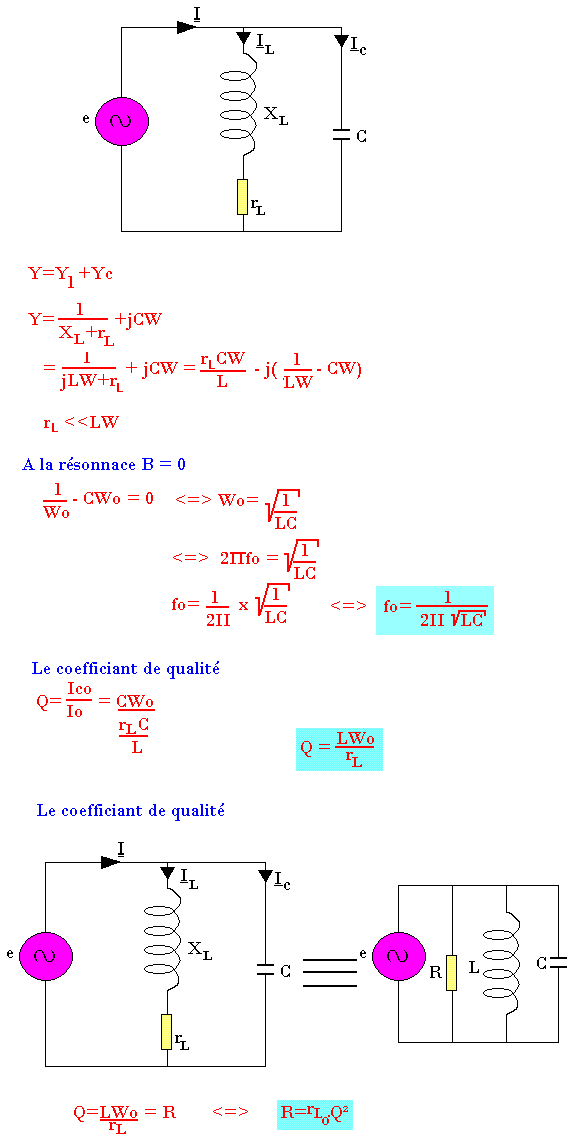
↔ Q = CRω = R/Lω
En réalité une bobine est un constituée d'une petite résistance rL en série avec une inductance pure d'impédance XL. Alors on est souvent amené à utiliser le circuit pratique suivant.