Compensation du facteur de puissance
Dans certaines applications de l'électronique, le facteur de puissance (CosÞ) est souvent trop petit et on a besoin de le ramener au tour de 1.
Comme le cosinus Þ est généralement arrière (circuit inductif), l'artifice consiste à mettre en parallèle avec le réseau un condensateur qui va annuler l'action Q existant.
Exercice:
V = 220V - 50Hz
P = 10KW
CosÞ = 0,66ARR
Calcul c pour CosÞ=0,93
Qinst = P.tgÞ avant la comparaison
Q'inst = P.tgÞ' = Qinst + Qc
CosÞ = 0,66 ↔ Þ = 48,7°
CosÞ' = 0,93° ↔ Þ' = 21,56°
Q'inst = P.tgÞ - V2.C.ω = P.tgÞ' ↔ P.tgÞ - P.tgÞ' = V2.C.ω
AL:
C = P(tgÞ-tgÞ')/V2ω
AN:
C = 10x103(1,13-0,39)/2202x314 = 4,8x10-
Etude de la résonance
Un dipôle est à la résonance si l'impédance de ce dipôle ou de ce circuit est purement résistif pour une fréquence f0 donnée appelée fréquence de résonance.
Soit Z cette impédance Z=a+jb
b=0 ; |Z|=a ; Þ=0° ou 180°
Etude des circuits RLC séries
Fréquence de résonance (f0)
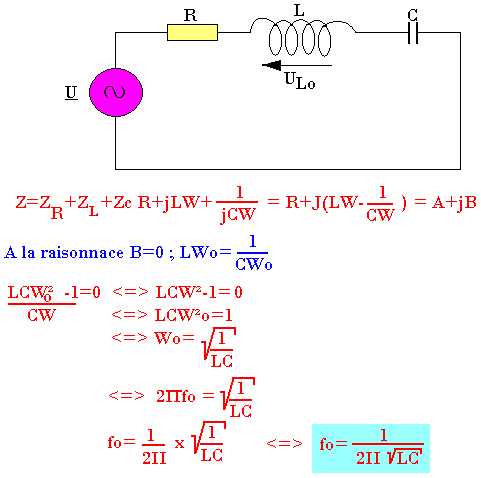
Quelques définitions
On appelle cœfficient de qualité Q le rapport entre la valeur maximale de l'énergie stockée par l'énergie dissipée par période.
Q = 2x3,14QS/QD
QS = ½LI2max = ½CV2max
QD = R(Imax/2½)2/f0
Pour les circuits en séries, le facteur de qualité Q est aussi le facteur de surtension pour les bobines. On a alors Q=ULo/U
ULo est la tension aux bornes de l'inductance à la fréquence de résonance. On a donc:
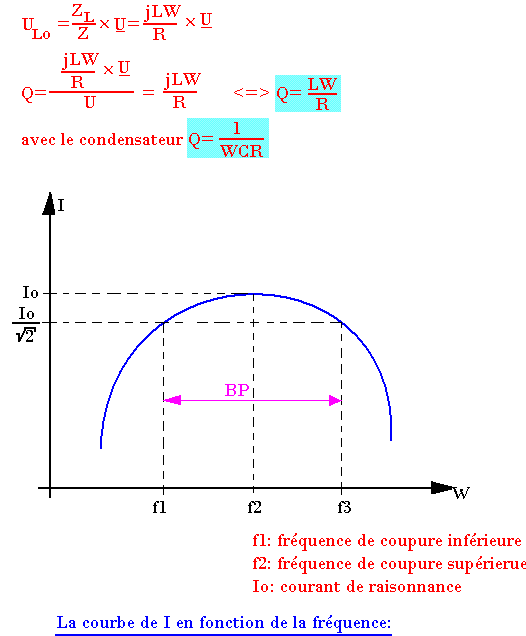
f1 et f2 sont définis pour I=I0/2½ c'est-à-dire à la moitié de la puissance active fournie bau réseau quand la fréquence est f0.
On montre que:
Q = ω0/(ω2-ω1) = f0/(f2-f1) = f0/BP avec BP:Bande passante
BP = f2 - f1
W0 = (ω1.ω2)½
f0 = (f1.f2)½
