Le courant alternatif monophasé - Relation tension courant dans les circuits R.L.C
Index de l'article
Relation tension courant dans les circuits R.L.C
Notion d'impédance
Notion de déphasage:
- DÞxy=|Þx-Þy|
- Si Þx-Þy>0; x est en avance sur y ou y est en retard sur x
- Si Þx-Þy<0; x est en retard sur y ou y est en avance sur x
- Si Þx-Þy=0; On dit que x et y sont en phase
- Si Þx-Þy=180° x et y sont en opposition de phase
- Si Þx-Þy=90°; x est en quadrature de d'avance sur y
- Si Þx-Þy=-90°; x est en quadrature de retard sur y
Notion d'impédance
Soit Z un nombre complexe, la loi d'ohm aux bornes d'un dipôle passif R.L.C est donnée par la relation suivante U=Z.I.
Z est l'angle de déphasage entre la tension U et le courant.
L'admittance Y est l'inverse de l'impédance T=1/Z, Y en siemens (s)
Cas d'une résistance
Exemple 1
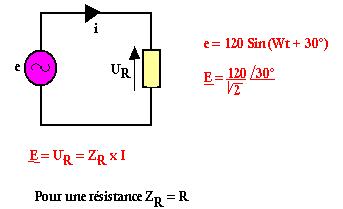
Dans une résistance le courant et la tension sont en phase.
Exemple 2
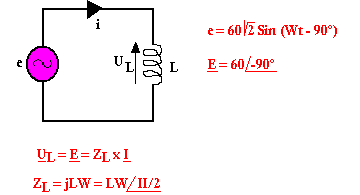
Ici la conclusion est simple, le déphasage entre les deux est de 90° et ici le courant est en retard sur la tension de 90°. Pour une inductance le courant est en retard sur la tension de 90°
Diagramme vectoriel
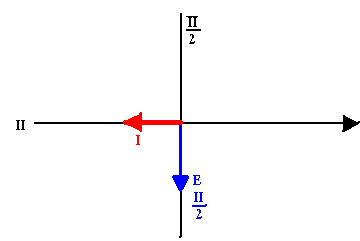
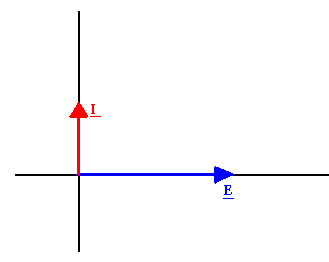
Cas d'un conducteur
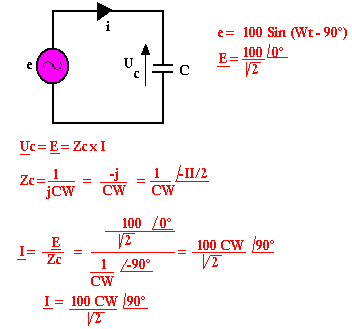
Le courant est en avance sur la tension de 90°
Diagramme vectoriel
Cas d'une résistance et inductance
En série
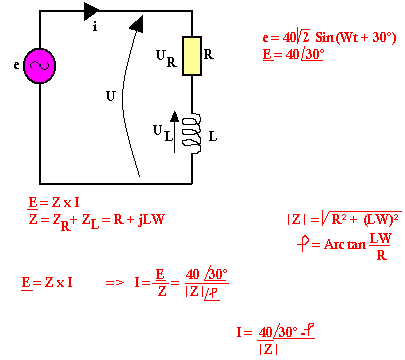
Par la maille
E - UL - UR = 0
E - ZL.I - ZR.I = 0
E = I(ZL + ZR)
E = I.Z
Diagramme vectoriel
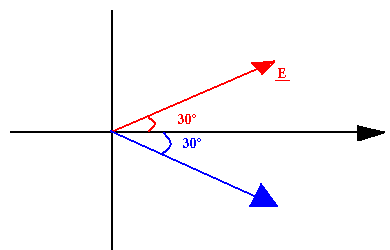
En parallèle
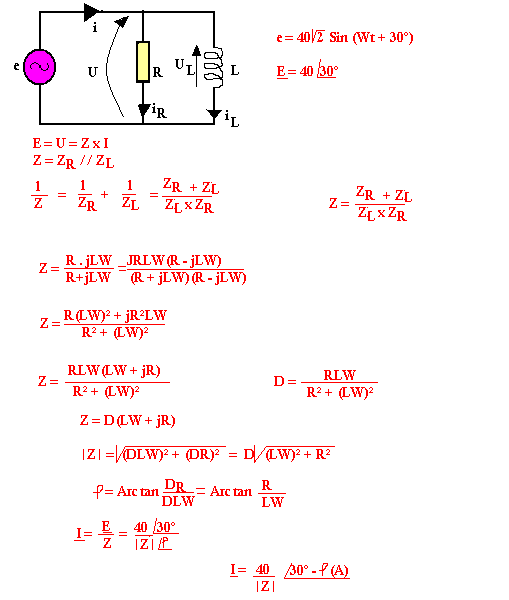
Puissance instantanée
On appelle puissance instantanée le produit de la tension et du courant instantané.
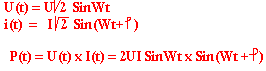
La puissance moyenne
La puissance moyenne est la moyenne de la puissance instantanée. Pour une sinusoïde on a:
P = U.ICosÞ
La puissance apparente complexe
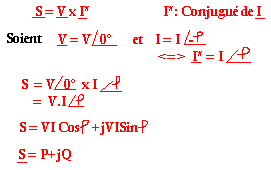
Avec:
- P = U.I.CosÞ (en Watt) puissance moyenne.
- Q = U.I.SinÞ (en VAR) puissance réactive
- S: puissance apparente complexe (en V.A)
![]()
Le triangle de puissance
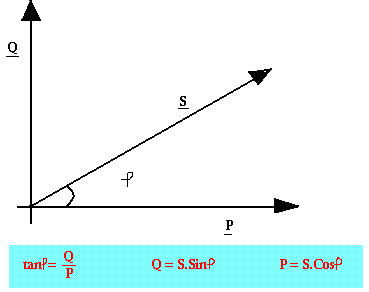
Le facteur de puissance
On appelle facteur de puissance noté FP, le rapport de la puissance moyenne sur la puissance apparente. Pour une sinusoïde, on a: FP=P/S=V.IcosÞ/V.I=CosÞ
↔ FP = CosÞ
