Droites parallèles
Deux droites sont parallèles lorsque leur interception est vide.
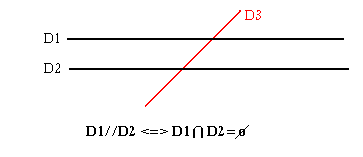
Théorème de Thalès
Des parallèles qui déterminent des segments égaux sur une sécante donnée déterminent aussi des segments égaux sur toutes autres sécantes.
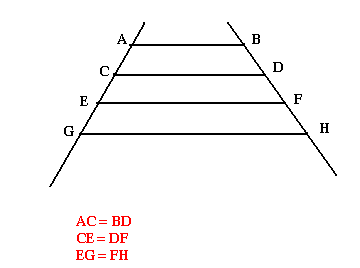
Théorème de Thalès appliqué au triangle
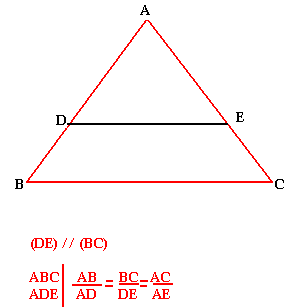
Dans un triangle, toute parallèle à un côté d'un triangle détermine sur les deux autres côtés des segments proportionnels
Théorème de Thalès
Figure clef
Dans un triangle, lorsqu'une droite est parallèle à l'un des côtés d'un triangle le théorème de Thalès s'impose dans les triangles suivants:
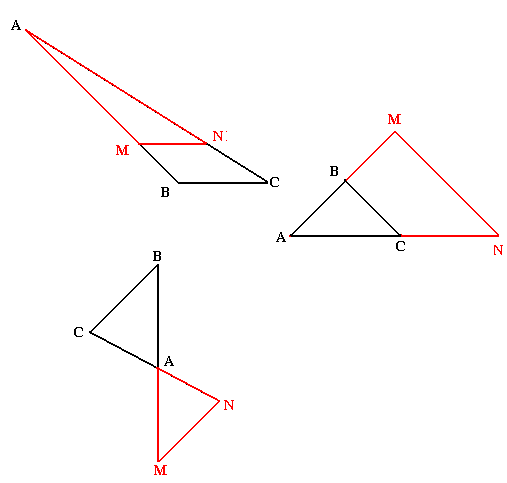
Dans tous les cas la droites (MN) est parallèle à la droite (BC) et la position de M par rapport à la droite (AB) étant la même que celle de N par rapport à la droite (AC), on peut écrire que le troisième quotient AM/AB=AN/AC est alors égale à MN/BC à chacun des quotients précédents, on peut écrire AM/AB=AN/AC=MN/BC car deux quantités égales à une même 3e sont égales entre elles alors a=b; c=b ↔ a=c.
Exemple:
Le triangle ABC étant un triangle, les droites (DE) et (BC) sont parallèles, en centimètre on a:
AD=30
AB=80
AC=120
1) Ecrivons le théorème de Thalès pour les triangles ADE et ABC.
2) Calculons AE en déduisons EC.
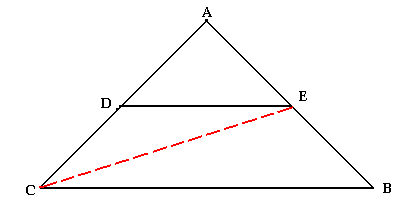
Théorème de Thalès
(DE)//(BC) ↔ ADE; ACB; AD/AC=DE/CB=AE/AB.
II.4. Calcul de AE
AD/AC = AE/AB = AD x AB = AC x AE
= AE = (AD x AB)/AC
AN:
AE = (30 x 80)/120
AE = 20
Déduction de EC
Le triangle ECB est un triangle isocèle, par conséquent EB=EC.
(BC)//(MN).
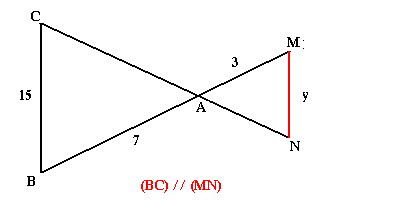
Calculons y:
d'après le théorème de Thalès.
ABC; AMN; AB/AM=BC/MN=AC/AN
AB/AM=BC/MN ↔ CB.AM=MN.AB
MN = (AM x BC)/AB
AN:
MN = (3 x 15)/7 = 45/7 = 6,428.
Cas particulier
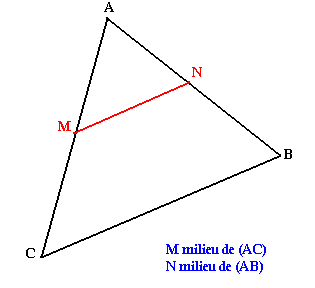
Soit un triangle ABC tel que M milieu de (AC) et N milieu de (AB). La droite (MN)//(BC), entraîne le théorème des milieux.
M milieu de (AC) et N milieu de (AB) alors MN//BC et MN=BC/2.
Théorème réciproque
Le théorème réciproque de Thalès veut démontrer que si les segments sont proportionnels, alors il existe une droite qui est parallèle à l'un des côtés du triangle.
Exemple
ABC est un triangle tel que AB=15 et AC=5 les points M et N appartiennent respectivement à AC et à AB tels que AM=3; AN=9. Montrons que les droites (MN) et (CB) sont parallèles.
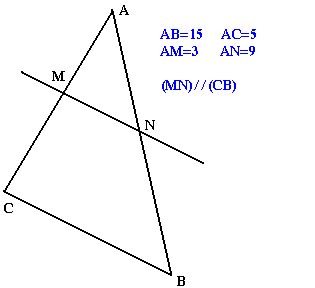
Si (MN)//(CB) alors d'après le théorème de Thalès on peut écrire que AMN; ACB; AM/AC=MN/CB=AN/AB
AM/AC=AN/AB ↔ 3/5=9/15
45 ↔ 45
Théorème de Thalès appliqué au trapèze
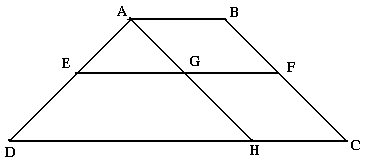
Soit un trapèze ABC et la droite (EF)//(DC) et à (AB), le théorème de Thalès permet d'écrire que les côtés sont proportionnels. AE/ED=BF/FC
Pour calculer la distance (EF) on trace une droite (AH)//(BC) tel que les côtés soient proportionnels.
Exemple:
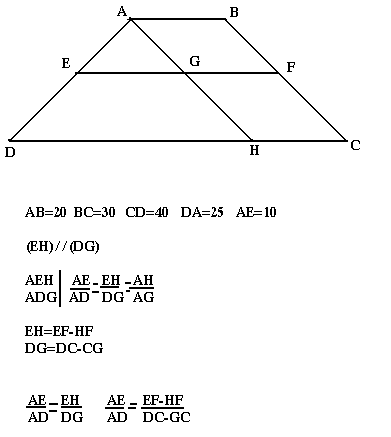
ABCD est un trapèze de (AB) et (CD) tel que (AB)=20; BC=30; CD=40; DA=25. Sur le côté (AD) on marque un point tel que AE=10, F est le point d'intersection de (BC) avec la droite parallèle à (AB) passant par E. Calculons (EF).
Triangles semblables
On appelle triangle semblable, des triangles qui se ressemblent donc qui s'assemblent. Deux ou plusieurs triangles sont semblables si et seulement si leur angles sont égaux chacun à chacun et si leurs côtés sont proportionnels.
Exemple
Soit un triangle ABC tel que (MN)//(BC) montrez que les triangles AMN et ABC sont semblables.
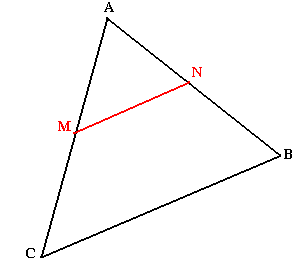
(MN)//(CB) alors il existe deux triangles AMN et ABC.
Ils ont  commun.
(MN)//(CB) d'après le théorème de Thalès on peut écrire que AM/AB=MN/BC=AN/AC, ce qui veut dire que les triangles sont semblables.
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale