Théorème de Thalès: application au triangle - Cas particulier

Cas particulier

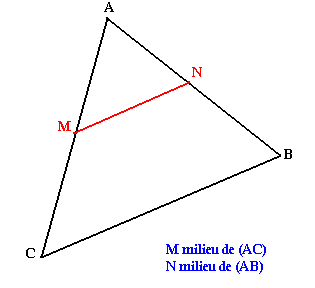
Soit un triangle ABC tel que M milieu de (AC) et N milieu de (AB). La droite (MN)//(BC), entraîne le théorème des milieux.
M milieu de (AC) et N milieu de (AB) alors MN//BC et MN=BC/2.

Théorème réciproque

Le théorème réciproque de Thalès veut démontrer que si les segments sont proportionnels, alors il existe une droite qui est parallèle à l'un des côtés du triangle.

Exemple

ABC est un triangle tel que AB=15 et AC=5 les points M et N appartiennent respectivement à AC et à AB tels que AM=3; AN=9. Montrons que les droites (MN) et (CB) sont parallèles.

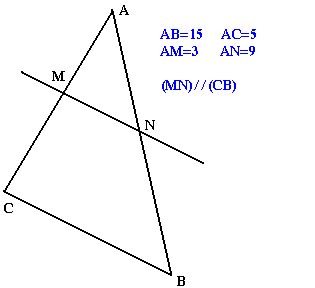
Si (MN)//(CB) alors d'après le théorème de Thalès on peut écrire que AMN; ACB; AM/AC=MN/CB=AN/AB
AM/AC=AN/AB ↔ 3/5=9/15
45 ↔ 45