Théorème de Thalès: application au triangle - Théorème de Thalès appliqué au trapèze

Théorème de Thalès appliqué au trapèze

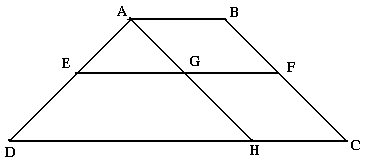
Soit un trapèze ABC et la droite (EF)//(DC) et à (AB), le théorème de Thalès permet d'écrire que les côtés sont proportionnels. AE/ED=BF/FC
Pour calculer la distance (EF) on trace une droite (AH)//(BC) tel que les côtés soient proportionnels.

Exemple:

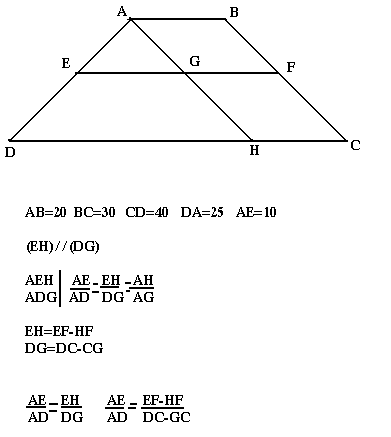
ABCD est un trapèze de (AB) et (CD) tel que (AB)=20; BC=30; CD=40; DA=25. Sur le côté (AD) on marque un point tel que AE=10, F est le point d'intersection de (BC) avec la droite parallèle à (AB) passant par E. Calculons (EF).

Triangles semblables

On appelle triangle semblable, des triangles qui se ressemblent donc qui s'assemblent. Deux ou plusieurs triangles sont semblables si et seulement si leur angles sont égaux chacun à chacun et si leurs côtés sont proportionnels.

Exemple

Soit un triangle ABC tel que (MN)//(BC) montrez que les triangles AMN et ABC sont semblables.

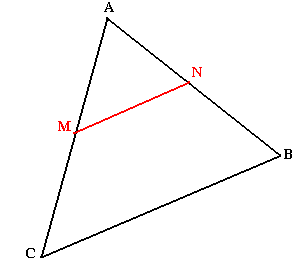
(MN)//(CB) alors il existe deux triangles AMN et ABC.
Ils ont  commun.
(MN)//(CB) d'après le théorème de Thalès on peut écrire que AM/AB=MN/BC=AN/AC, ce qui veut dire que les triangles sont semblables.