Théorème de Thalès: application au triangle - Théorème de Thalès

Théorème de Thalès

Figure clef

Dans un triangle, lorsqu'une droite est parallèle à l'un des côtés d'un triangle le théorème de Thalès s'impose dans les triangles suivants:

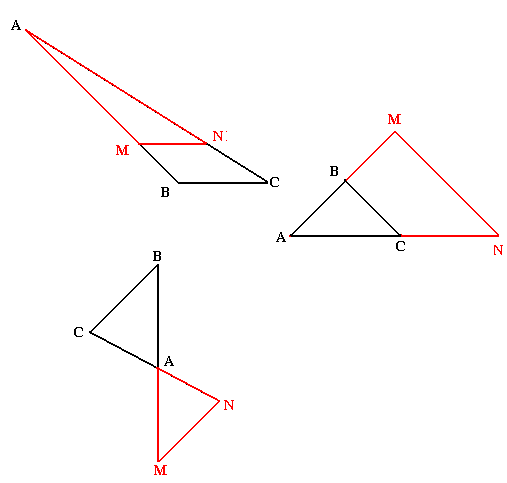
Dans tous les cas la droites (MN) est parallèle à la droite (BC) et la position de M par rapport à la droite (AB) étant la même que celle de N par rapport à la droite (AC), on peut écrire que le troisième quotient AM/AB=AN/AC est alors égale à MN/BC à chacun des quotients précédents, on peut écrire AM/AB=AN/AC=MN/BC car deux quantités égales à une même 3^e sont égales entre elles alors a=b; c=b ↔ a=c.

Exemple:

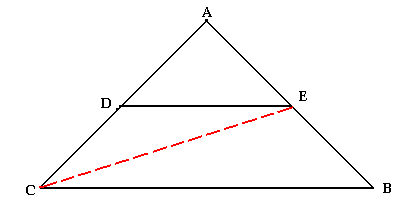
Le triangle ABC étant un triangle, les droites (DE) et (BC) sont parallèles, en centimètre on a:
AD=30
AB=80
AC=120
1) Ecrivons le théorème de Thalès pour les triangles ADE et ABC.
2) Calculons AE en déduisons EC.

Théorème de Thalès

(DE)//(BC) ↔ ADE; ACB; AD/AC=DE/CB=AE/AB.

II.4. Calcul de AE

AD/AC = AE/AB = AD x AB = AC x AE
= AE = (AD x AB)/AC

AN:
AE = (30 x 80)/120
AE = 20

---

Déduction de EC

Le triangle ECB est un triangle isocèle, par conséquent EB=EC.
(BC)//(MN).

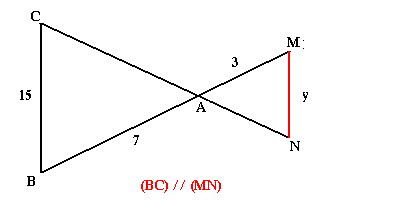
Calculons y:
d'après le théorème de Thalès.
ABC; AMN; AB/AM=BC/MN=AC/AN
AB/AM=BC/MN ↔ CB.AM=MN.AB
MN = (AM x BC)/AB
AN:
MN = (3 x 15)/7 = 45/7 = 6,428.