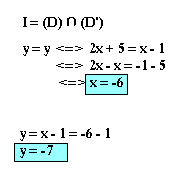L'équation de droite passant par deux points A et B quelconques est de la forme y=ax+b, oú a est appelé coefficient directeur ou la pente et b est appelé l'ordonné à l'origine. L'équation de la droite passant par deux points se présente sur deux formes:
- ax+by+c=0 (la forme explicite)
- y=ax+b (forme implicite)
Pour écrire l'équation de droite passant par deux points A et B quelconque (équation cartésienne) on suppose un troisième point M de coordonné (x; y) tel que AM et AB colinéaire (det (AM; AB)=0)
Exemple
Ecrivons de droite passant par deux points A et B, on suppose sur troisième point M(x; y).
A(1; 2); B(3; 4).
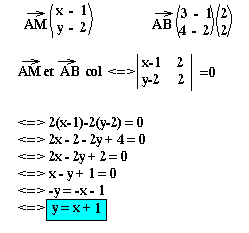
Point appartenant à une droite
Soit une droite (D) et un point A quelconque. Le point A appartient à la droite (D) si et seulement si les coordonnés de A vérifient les équations de la droite (D).
Exemple
Soit la droite d'équation (D) d'équation 2x-y+3=0 et des points A(-1; 1); B(0; 3); C(½; -4); D(1; 2); E(0; 1). A, B et C. A, B et B appartiennent à (D).
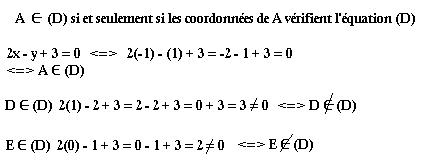
Equation de droite passant par deux points ayant un vecteur directeur "u"
Pour écrire une équation de droite passant par deux points A et B ayant un vecteur directeur u, on détermine le vecteur AB de telle manière que le vecteur AB soit colinéaire.
Exemple
Soit une droite (D) d'équation 3x+2y+4=0
1) Quel est la pente de cette droite.
2) Le point A de coordonnés 5 et b appartient à la droite (D). Calculez b.
A(5; b)
A appartient à (D) ↔ 3(5)-2b+4=0
↔ 15-2b+4=0
↔ 19-2b=0
↔ +2b=+19
↔ b=19/2
Recherche de la pente
3x-2y+4=0
+2y=+3x+4
y=(3x+4)/2 ↔ y=3x/2+2
la pente est égale à 3/2.
Droites parallèles
Deux droites sont parallèles lorsque leur interception est vide.
(D)//(D') ↔ (D) inclue dans (D') = Ø.
Soient deux droites (D) et (D') l'équation:
(D): y=ax+b
(D'): y=a'x+b'
On dit que (D)//(D') si et seulement si a=a'. En somme deux droites sont parallèles lorsqu'elles ont même coefficient angulaire.
Exercice:
(AB) y-x+3=0
(CD) y=x-4
Montrez que (AB) et (CD') sont parallèles
(AB) y-x+3=0 ↔ y=x-3
↔ a=1
(CD) y=x-4 ↔ a'=1
alors a=a' ↔ (AB)//(CD)
Points appartenant à la droite
Soit la droite (D) d'équation y=ax+b et un point A quelconque. A appartient à (D) si et seulement si les coordonnées de A vérifient l'équation de la droite (D).
Exercice
Soit la droite (D) d'équation (D):y+3-3=0
A(1; 2); B(3; 0); C(1; -1); D(0; 4)
Montrez que A et B appartiennent à la droite (D) et C n'appartient par à la (D).
La droite (D) appartient-il à la droite (D). Justifiez.
Application
(D): y+x-3=0
A appartient à (D) si et seulement si ses coordonnées vérifient l'équation de (D)
A(1; 2) ↔ 2+1-3=0
A appartient à (D)
B(3; 0) ↔ 0=-3+3 ↔ B appartient à (D)
C(1; -1) ↔ -1=-1+3=2 -1≠2
C n'appartient pas à (D)
D(0; 4) ↔ 4=0+3 4≠3
D n'appartient pas à (D)
Droites perpendiculaires
Soient (D): y=ax+b
(D'): y=a'x+b
(D) perpendiculaire à (D') si et seulement si (D) est inclue dans (D')=90°
Deux droites sont perpendiculaires si et seulement si le produit de leur coefficient angulaire est égale à -1. (D) perpendiculaire à (D') implique que axa'=-1.
Exercice
(D1): y=x+2 → a1=1
(D2): y=-x-4 → a2=-1
(D3): y=x+7 → a3=1
a1=a3=1 ↔ (D3)//(D3)
a1xa2=(1)(-1)=-1 ↔ (D1) perpendiculaire à (D2)
↔ (D2) perpendiculaire à (D3)
Représentation graphique d'une droite
Une droite (D) ne peut passer que par au moins par deux points. Représenter graphiquement la droite d'équation y=ax+b revient à trouver deux points a et b qui appartiennent à cette droite.
Exemple 1
Représentez graphiquement la droite (D): y=x+1
|
x |
0 |
-1 |
|
y |
1 |
0 |
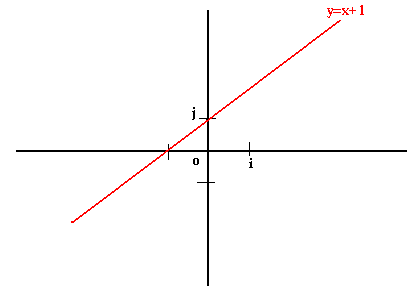
Exemple 2
(D): y=2x-3
|
x |
0 |
3/2 |
|
y |
-3 |
0 |
(D'): y=-½x+1
|
x |
0 |
2 |
|
y |
1 |
0 |
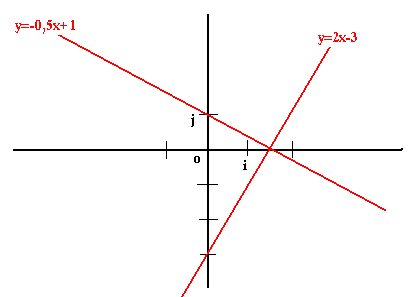
Point d'interception
On appelle point d'interception le point de rencontre de deux ou plusieurs droites. Soit deux droites (D) et (D') et I leur point d'interception. On a:
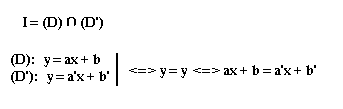
Exemple
Soient (D): y=2x+5
(D'): y=x-1
déterminez les coordonnées de I et le point d'interception.
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale