Les lignes de niveau

Etant donné une application f du plan P dans R et K un nombre réel. On appelle ligne de niveau K de f l'ensemble des points donc l'image par f est K.

Détermination des lignes de niveau A. Ligne de niveau de l'application M→AM.AB

Etant donné deux points A et B du plan et f l'application de P dans R qui à tout point M associe AM.AB. La ligne de niveau (L_K) est l'ensemble des points M du plan tel que f(M)=K c'est-à-dire AM.AB=K.

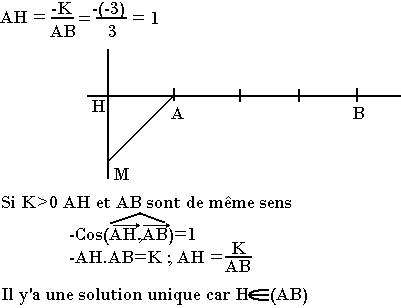
Exemple 1:

On donne AB=3 ; K=3
Calculez la ligne de niveau (L-3)

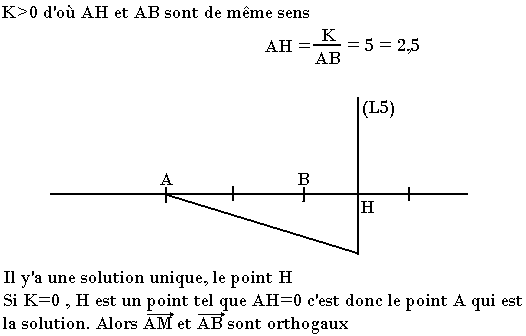
Exemple 2:

AB=2 ; K=5 Déterminez la ligne de niveau (L5)

Exemple 3:

AB=4 ; K=0 H est un point tel que AH=0. H se confond donc avec le point A. Les vecteurs AM et AB sont orthogonaux