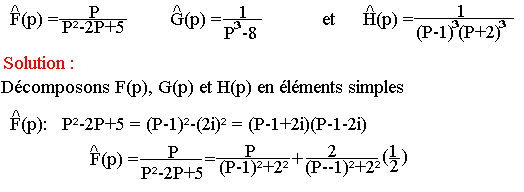Série de Fourier
Intégration de fonctions paires ou impaires
Cas d'une fonction paire
Soit P(x) une fonction continue par morceau et paire sur un intervalle U= [-a; +a]
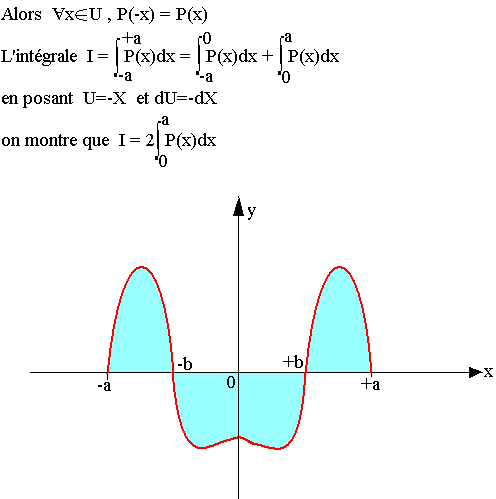
"L'intégrale d'une fonction paire sur un intervalle symétrique est le double de l'intégrale calculée sur la moitié de l'intervalle"
Cas d'une fonction impaire
Soit une fonction continue par morceau et impaire sur un intervalle V= [-h; +h].
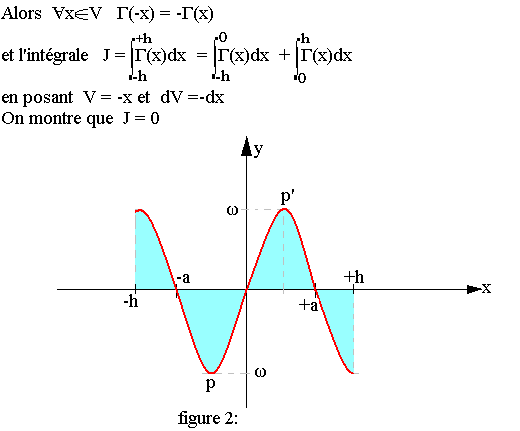
"L'intégrale d'une fonction impaire sur un intervalle symétrique est nulle"
Série trigonométrique de Fourrier
Soit f une fonction sur un intervalle [-l; +l]. On appelle série de Fourrier de f notée S.F(f).
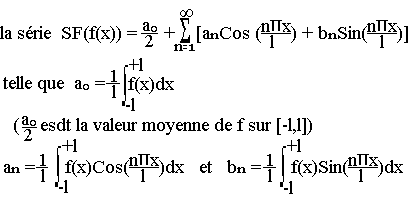
Cas d'une fonction 2l périodique
Si f est une fonction périodique de période T=2l alors (f(x)) est développable sur un intervalle symétrique ou non symétrique de diamètre T.
Exercice :
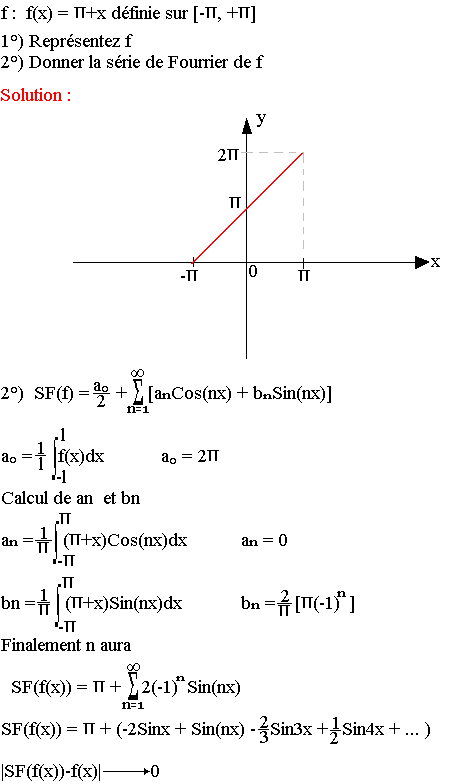
Remarque:
SF (ƒ(x)) aux points de discontinuité de première espèce
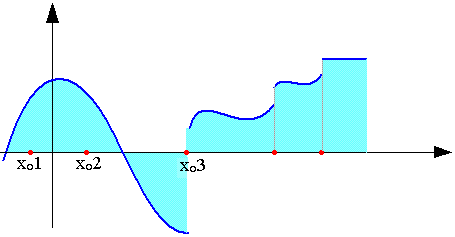
Si f présente les points de discontinuité de première espèce en x0; x02; x03;... ; x0n alors
![]()
Propriétés:
Si f est paire les cœfficient bn de SF(ƒ) sont tous nuls.
Si f est impaire alors les coefficients an de
Cas de fonctions non périodique
Soit g une fonction quelconque définie sur un intervalle [a, b], alors on peut définir la série de Fourrier de g par deux méthodes simples:
Première période:
On peut choisir un intervalle symétrique [-h; +h] < [a, b] et établir SF(g(x)) sur [-h; +h].
Deuxième période:
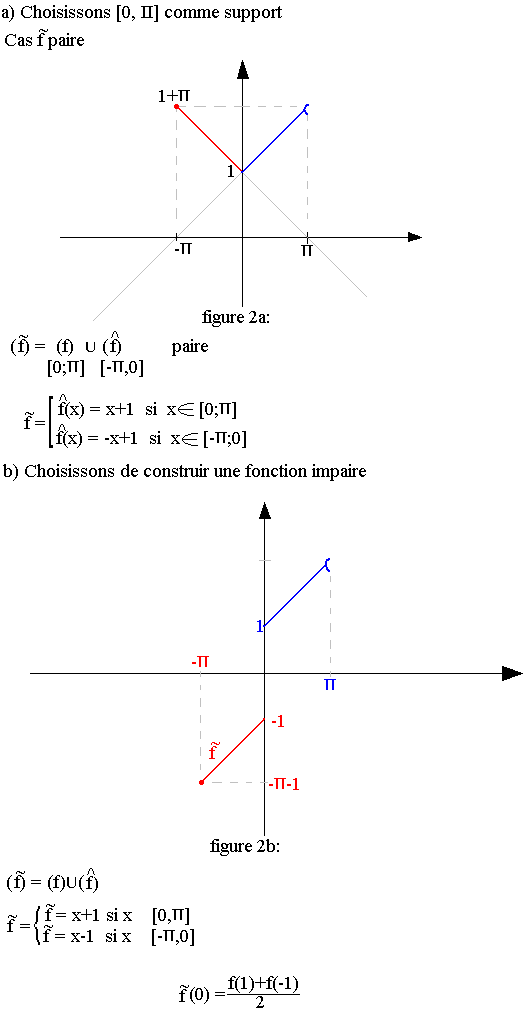
On peut choisir un intervalle [a, k] et utiliser la restriction de g sur [0, k] puis établir un prolongement g sur [-k; 0] telle que la nouvelle courbe ainsi construite soit paire ou impaire.
Exemple:
Soit f(x)=x+1
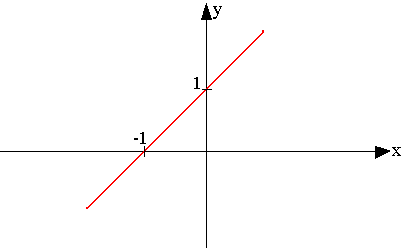
Choisissons un intervalle symétrique par exemple
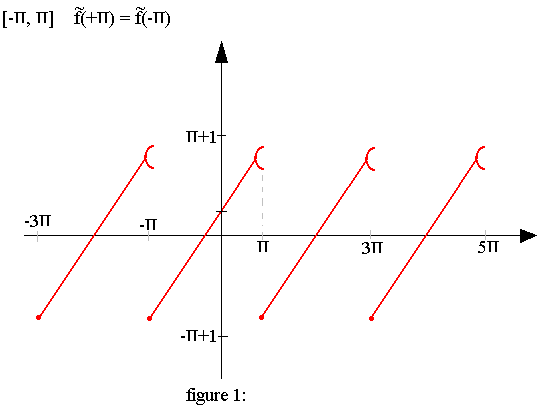
ƒ(x) = x+1
Condition de Dirichlet
Une fonction f définie sur [a, b] vérifie les conditions de Dirichlet si (i) et (ii)
(i) La courbe de f (Cƒ) admet un nombre fini d'extrema sur [a,b].
(ii) Si f admet les points de discontinuité, alors ceux-ci sont de première espèce.
Conclusion:
Une fonction est dérivable en série de Fourrier sur [a, b] si elle vérifie les conditions de Dirichlet auquel cas:
- SF(ƒ(x))=ƒ(x) en dehors des points (xi) de discontinuité.
- Aux points de discontinuité (xi). SF(xi)=½[ƒ(x-i)+f(x+i)
- Si f est 2l périodique SF(x-l)=SF(x+l) lorsque a=l et b=+l
Transformée de Fourrier
Notion d'intégrale double
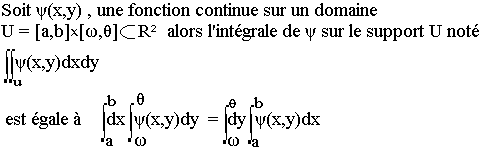
Exemple:
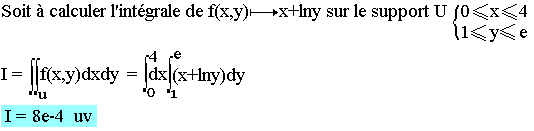
On a vu que la série de Fourrier d'une fonction f, 2l périodique ou non s'écrit:

Formule complexe de f(x)
(4) peut aussi s'écrire sous forme complexe

Transformation de Fourrier inverse
Soit F(h) la transformée de Fourrier de f(x) alors f(x) est la transformée inverse de F(h)
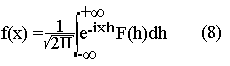
La transformation de Fourrier est une opération bijective, elle permet les opérations de codage de flux de signaux.
Transformée de Laplace
Recherche de la transformée (image) d'une fonction
Soit F(t) une fonction qui satisfait aux 3 conditions suivantes:
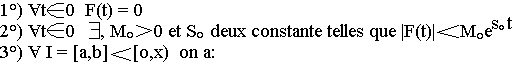
- F(t) est bornée
- F(t) est continue sur I ou alors présente un nombre fini de points de discontinuité de première espèce.
- F(t) présente un nombre fini extrema
Alors F(t) est transformable selon Laplace et la transformée de fonction selon Laplace est l'intégrale notée:
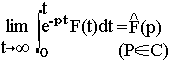
Condition aux points de discontinuité
Si F(t) présente, un point de discontinuité ti alors on aura:
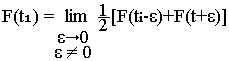
Propriétés
Soit F(t) admet une image (transformée) F(P) alors son origine (transformée inverse) F0(t) est unique et inversement.
A toute combinaison linéaire d'un ensemble fini de fonction, on peut faire correspondre la combinaison linéaire des transformées de ces fonctions.
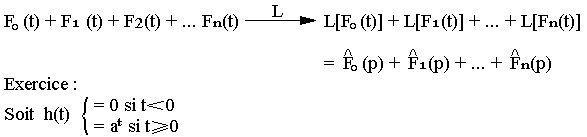
- Déterminez la transformée de Laplace de h(t)
- Déterminez sa transformée de Fourrier de W(t)=at quelque soit t appartenant à R
Recherche de l'origine
Inversement connaissant l'image d'une fonction F(P), on pourrait retrouver l'origine F(t) (opération de décodage). En pratique les outils mathématiques nécessaires seront:
- Les identités remarquables classiques: (a+b)2=a2+2ab+b2 ; (a3-b2)=(a-b)(a2+ab+b2) ; (1-PN)=(1-P)(1+P+P2+...+PN-1)
- Les méthodes de décomposition de fraction rationnelles en éléments simples.
Exemples :
Trouver les origines des transformées suivantes: