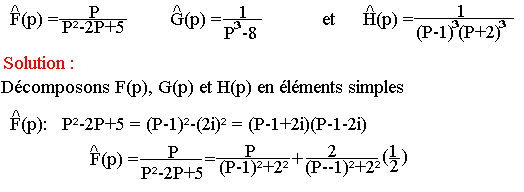Page 3 sur 3
Transformée de Laplace
Recherche de la transformée (image) d'une fonction
Soit F(t) une fonction qui satisfait aux 3 conditions suivantes:
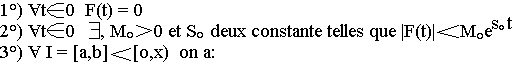
- F(t) est bornée
- F(t) est continue sur I ou alors présente un nombre fini de points de discontinuité de première espèce.
- F(t) présente un nombre fini extrema
Alors F(t) est transformable selon Laplace et la transformée de fonction selon Laplace est l'intégrale notée:
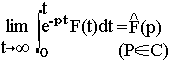
Condition aux points de discontinuité
Si F(t) présente, un point de discontinuité ti alors on aura:
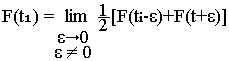
Propriétés
Soit F(t) admet une image (transformée) F(P) alors son origine (transformée inverse) F0(t) est unique et inversement.
A toute combinaison linéaire d'un ensemble fini de fonction, on peut faire correspondre la combinaison linéaire des transformées de ces fonctions.
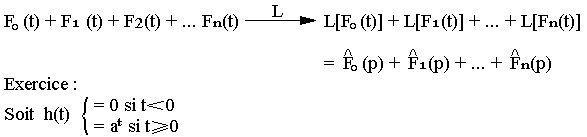
- Déterminez la transformée de Laplace de h(t)
- Déterminez sa transformée de Fourrier de W(t)=at quelque soit t appartenant à R
Recherche de l'origine
Inversement connaissant l'image d'une fonction F(P), on pourrait retrouver l'origine F(t) (opération de décodage). En pratique les outils mathématiques nécessaires seront:
- Les identités remarquables classiques: (a+b)2=a2+2ab+b2 ; (a3-b2)=(a-b)(a2+ab+b2) ; (1-PN)=(1-P)(1+P+P2+...+PN-1)
- Les méthodes de décomposition de fraction rationnelles en éléments simples.
Exemples :
Trouver les origines des transformées suivantes:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale