Opération sur les vecteurs
Produit scalaire
On donne les vecteurs V1 et V2, le produit scalaire de ces deux vecteurs est donné par:
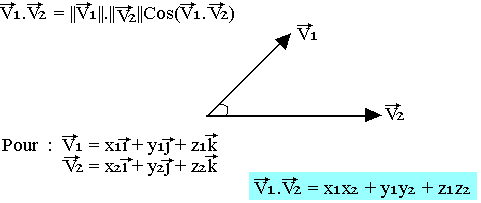
Produit vectoriel
Le vecteur V est un pseudo vecteur défini par convention tel que (V1, V2, W) soit un trièdre. L'une des propriétés du produit vectoriel est qu'il est anticommutatif c'est-à-dire que:
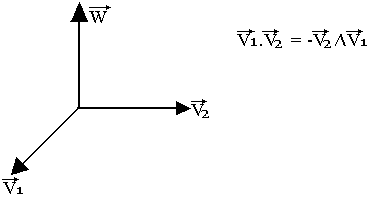
Il est associatif par rapport à la multiplication par les nombres, c'est-à-dire:
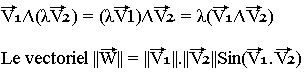
représente la surface du parallélogramme construit sur les vecteurs V1 et V2 et le vecteur W est toujours perpendiculaire à ce plan.
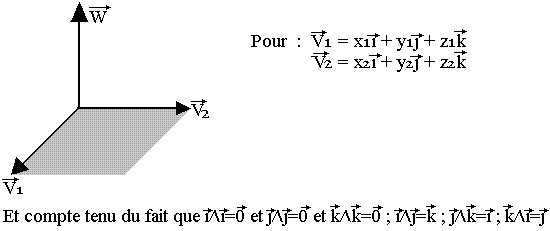
On a:
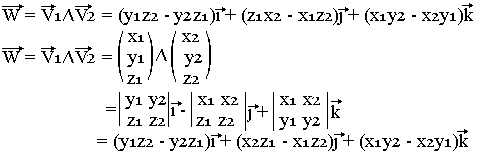
Double produit vectoriel
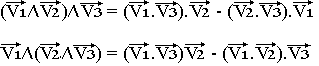
Champ de vecteurs
On appelle champ vectoriel un espace ou une portion d'espace où l'on peut définir en tout point un vecteur fonction de ce point. Si a(M) est le vecteur caractéristique du champ alors ce vecteur est fonction du point M. Ainsi on observe un vecteur dans lequel une charge électrique est soumise à une force électrique et on parle de champ électrique E(M).
Gradian d'une fonction scalaire
Soit ƒ(M) une fonction du point M appelle gradian de f que l'on note gradƒ, le vecteur défini par:
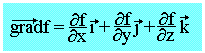
Divergence d'un champ de vecteur
On appelle divergence de a(M) le scalaire obtenu en faisant la somme des dérivées des composantes, suivant les axes par rapport aux variables correspondantes.
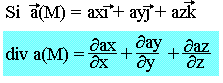
Rotationnel d'un champ de vecteur
On appelle rotationnel du point A, le vecteur donc les composantes cartésiennes ont pour expression respective
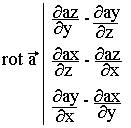
Appelons Nabla le pseudo vecteur ou vecteur symbolique donné par:
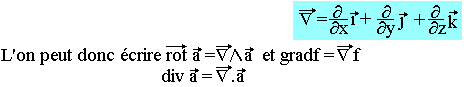
Opérateur Laplacien
On appelle Laplacien d'une fonction scalaire f(x, y, z), le scalaire donné par:
![]()
Ainsi, la divergence du gradian de f
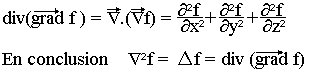
Le Laplacien d'un champ vecteur quant à lui est tel que pour
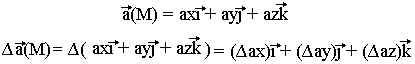
Flux d'un champ de vecteur
Considérons une surface S et un point M appartenant à (S), sur cette surface on délimite au tour de M un élément de surface ds.
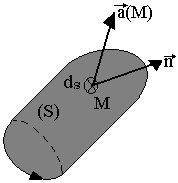
On appelle flux élément du vecteur a à travers ds le scalaire
![]()
n est la normale positive en M à la surface (S)
Le flux total à travers la surface (S) est donc
![]()
Flux conservatif: théorème de GREEN OSTROGRADSKI
On montre que pour tout vecteur à flux conservatif le flux à travers toute surface fermée est nul. Pour obtenir la condition pour qu'un champ vecteur soit à flux conservatif, on utilise le théorème de GREEN OSTROGRADSKI.
Théorème:
Le flux d'un champ vecteur à travers une surface fermée est égal à l'intégrale de ce champ vecteur étendu au volume intérieur à la surface.
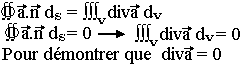
Circulation d'un champ de vecteur
Soit dans un champ vecteur un arc de courbe donc les extrémités sont A et B. Soit a(M) le vecteur du champ en un point M. On appelle circulation élémentaire de A le scalaire
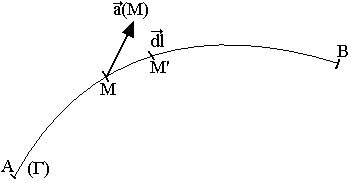
La circulation dépend généralement du chemin suivi pour aller d'un point à un autre. Cependant dans certains cas la circulation d'un vecteur entre 2 points donnés ne dépend que de la position de ces points et non du chemin suivi. La circulation du vecteur est en ces conditions nulle pour tous les vecteurs fermés. On dit que le champ vecteur dérive d'un potentiel.
Supposons que le vecteur a dérive d'un potentiel. Sa circulation entre un point M.

Théorème de STOKES:
La circulation d'un vecteur le long d'une courbe fermée est égale au flux du rotationnel de ce vecteur à travers toute surface.
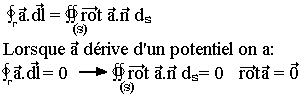
C'est la condition nécessaire et suffisante pour que a dérive d'un potentiel.
Lignes de vecteurs
On appelle ligne de vecteur ou ligne de champ, une courbe tangente dans chacun de ses points au vecteur caractéristique du champ.
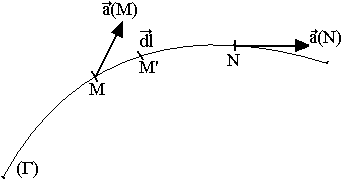
On obtient l'équation ds lignes de champ en écrivant qu'un déplacement élémentaire dl=MM' effectué à partir d'un point M sur la ligne de champ et parallèle au vecteur de ce champ.
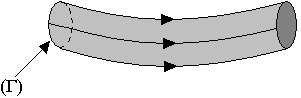
Tube de vecteurs
C'est l'ensemble de ligne de vecteur qui s'appuie sur une courbe fermée.
Autres systèmes de coordonnées
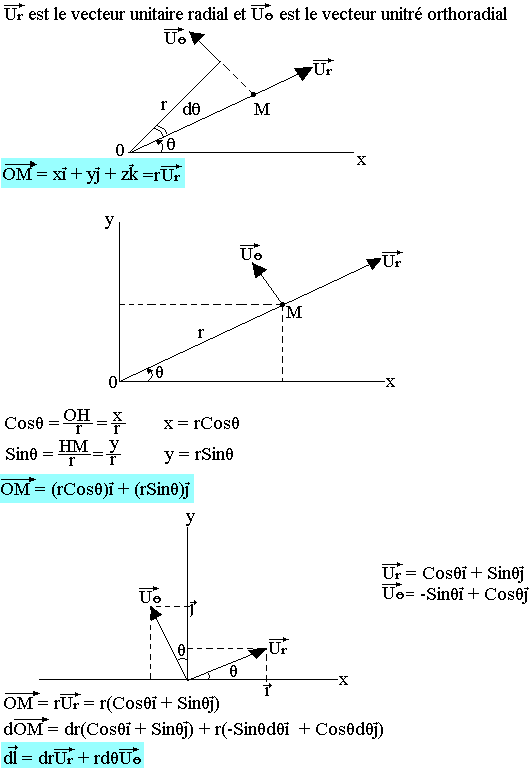
Coordonnées polaires
Soit M un point du plan et O une origine arbitraire. Dans ce cas r et l'angle balayé sont les coordonnées polaires de M.
Le point M dans ce cas est déterminé si on connaît la projection de n de M dans les axes (ox, oy) et la côte z de m au-dessus du plan.
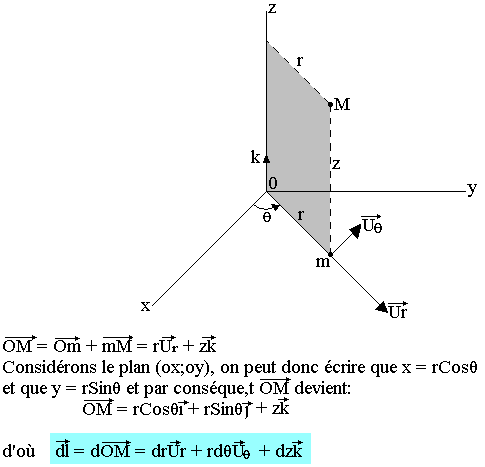
Coordonnées sphériques
On doit connaître le rayon r de la sphère, l'angle (OZ, OM), la projection m de M dans le plan (ox,oy) cette projection est déterminée par l'angle þ=(os,om).
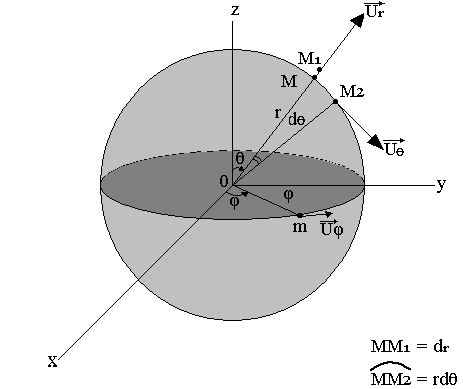
Vecteur unitaire
- Le vecteur Ur est dirigé suivant le vecteur MM1 ou ON. Le déplacement élémentaire de M est alors dl1=dr
- Lorsque θ varie seul M se déplace dans le plan (OZ, OM) suivant l'arc de cercle de centre O et de rayon r le déplacement élémentaire est: dl2=rdθ
- Lorsque þ varie tout seul, m décrit dans le plan (ox, oy) l'arc de cercle de centre O et rayon þ=om. M se déplace dans le plan parallèle à (ox, oy) passant par m
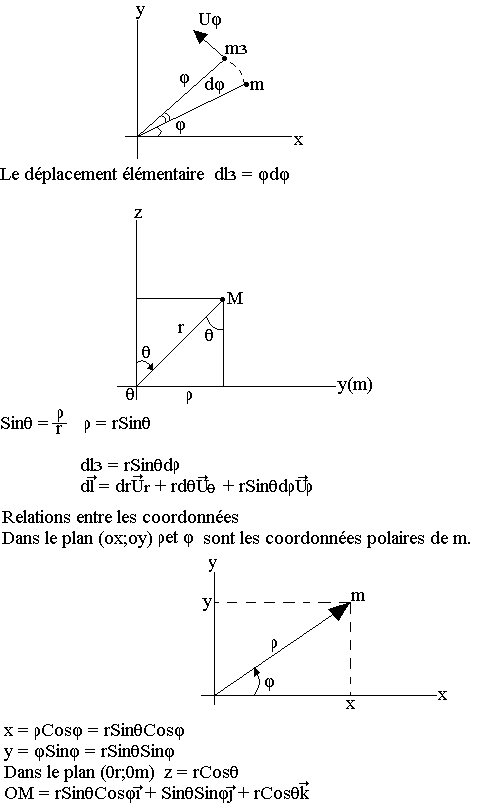
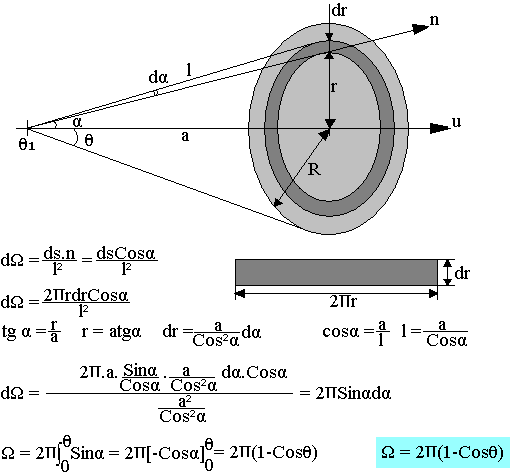
Notion d'angle solide
L'angle solide caractérise la portion d'espace que l'on peut voir d'un point donné à travers une surface. Soit un point O donné et une surface (S). Délimitons au tour d'un point M appartenant à (S) un élément de surface ds. La portion d'espace que du point O, on peut voir à travers ds, est intérieur au cône de sommet O, et donc la génératrice s'appuie sur le contour de ds.
Le cône précédent détermine sur cette sphère une surface dr qui est par convention la mesure de l'angle solide cherchée.
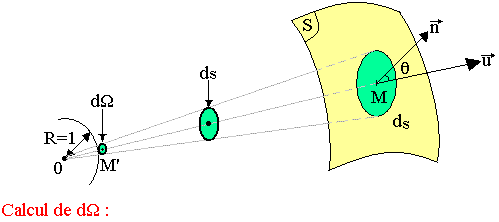
Calcul de dr
- dr est dans le pan tangent en M' à la sphère.
- ds n'est pas forcement dans le plan perpendiculaire à OM. On peut toujours considérer la projection de ds dans le plan perpendiculaire à OM et passant par M. On peut donc écrire
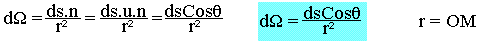
Pour une surface finie (S)
Exemple:
Calcul de l'angle solide sous lequel d'un point de son axe, on voit un disque de rayon R.
Pour calculer l'angle solide du disque vu d'un point de son axe O1, il faut d'abord calculer l'angle solide élémentaire dr sous lequel on voit une couronne élémentaire.