Autres systèmes de coordonnées

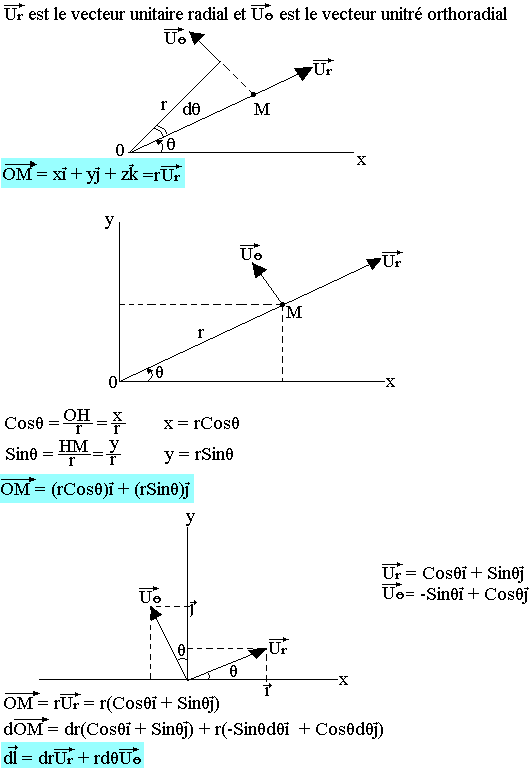
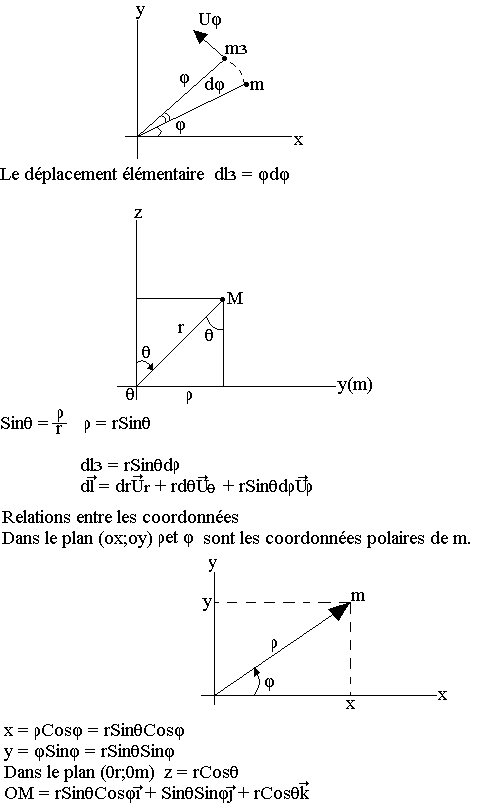
Coordonnées polaires

Soit M un point du plan et O une origine arbitraire. Dans ce cas r et l'angle balayé sont les coordonnées polaires de M.

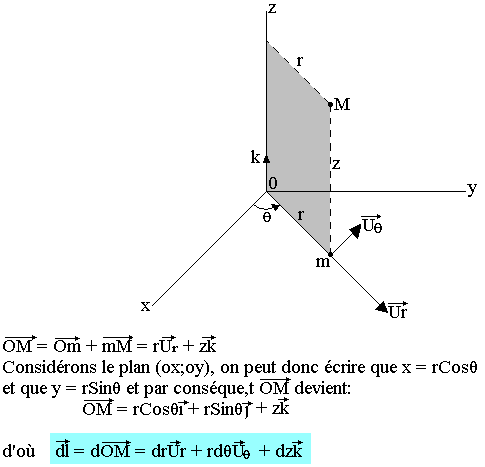
Le point M dans ce cas est déterminé si on connaît la projection de n de M dans les axes (ox, oy) et la côte z de m au-dessus du plan.

Coordonnées sphériques

On doit connaître le rayon r de la sphère, l'angle (OZ, OM), la projection m de M dans le plan (ox,oy) cette projection est déterminée par l'angle þ=(os,om).

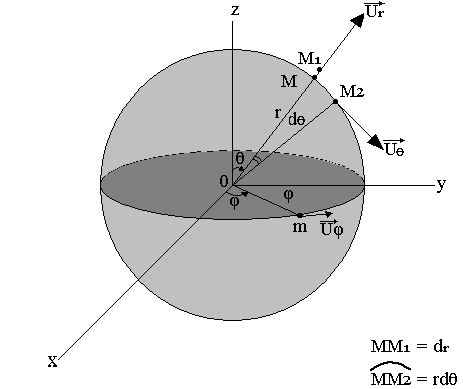
Vecteur unitaire

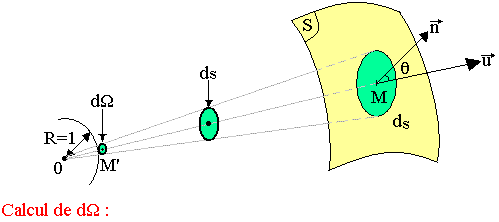
Notion d'angle solide

L'angle solide caractérise la portion d'espace que l'on peut voir d'un point donné à travers une surface. Soit un point O donné et une surface (S). Délimitons au tour d'un point M appartenant à (S) un élément de surface ds. La portion d'espace que du point O, on peut voir à travers ds, est intérieur au cône de sommet O, et donc la génératrice s'appuie sur le contour de ds.
Le cône précédent détermine sur cette sphère une surface dr qui est par convention la mesure de l'angle solide cherchée.

Calcul de dr

• dr est dans le pan tangent en M' à la sphère.
• ds n'est pas forcement dans le plan perpendiculaire à OM. On peut toujours considérer la projection de ds dans le plan perpendiculaire à OM et passant par M. On peut donc écrire
  
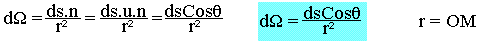
  Pour une surface finie (S)

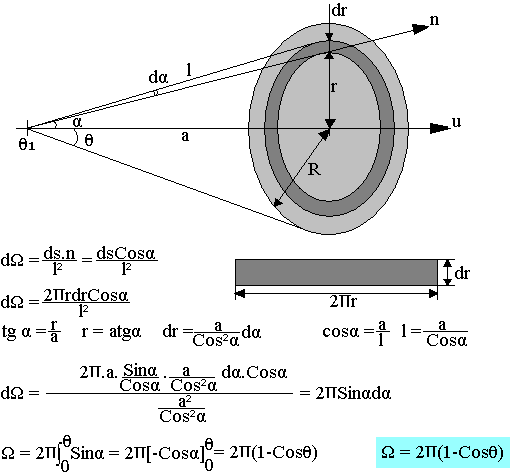
Exemple:

Calcul de l'angle solide sous lequel d'un point de son axe, on voit un disque de rayon R.
Pour calculer l'angle solide du disque vu d'un point de son axe O₁, il faut d'abord calculer l'angle solide élémentaire dr sous lequel on voit une couronne élémentaire.