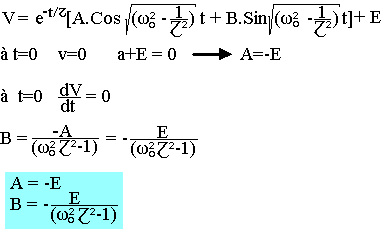Préambule
Dans ce cours nous nous proposons d'étudier les réponses de quelques circuits simples à une excitation sous forme d'un échelon.
Réponse d'un circuit à une excitation
Considérons un circuit à priori quelconque soumis à une excitation a(t). Cette excitation peut être une excitation en tension exercée par un générateur de tension convenable ou une excitation en courant exercée alors par un générateur de courant. Le circuit réagit à l'excitation et l'on appelle réponse du circuit une grandeur physique r(t) déterminée: tension ou courant mesuré en un pont du circuit. Nous allons examiner successivement les deux types de tension.
Echelon de tension
Réponse d'un circuit RC à un échelon de tension
Considérons le circuit suivant et supposons qu'à l'instant t=0 on ferme l'interrupteur K, le condensateur C étant initialement non chargé.
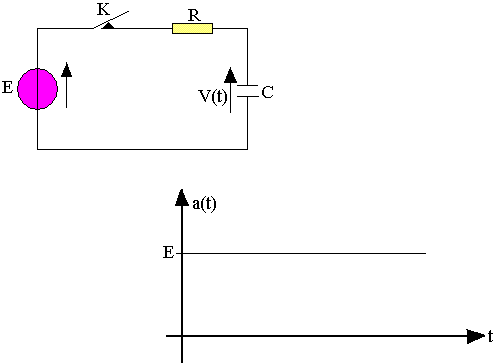
La réponse étudiée est la tension v(t) aux bornes du condensateur, où l'intensité I traversant le circuit. Par application des lois des mailles on obtient:
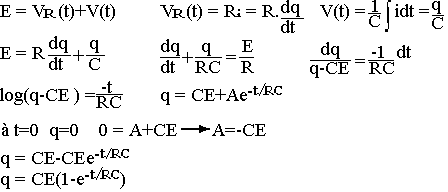
On définit la constante égale à RC comme la constante de temps du circuit:
Réponse en tension
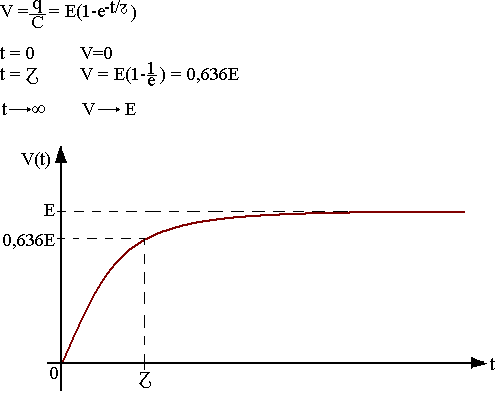
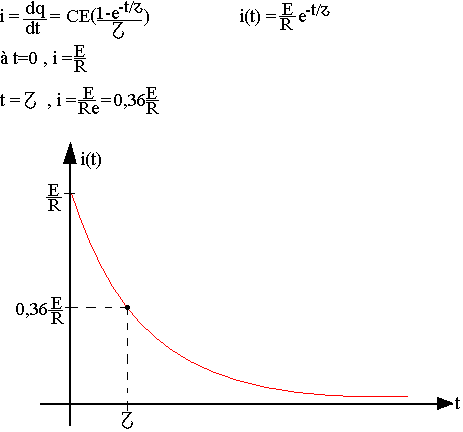
Réponse en courant
Bilan énergétique
Entre les instants 0 et t1>0, le générateur fournit l'énergie Wg telle que:
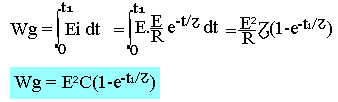
L'énergie dissipée dans R sous forme de chaleur est:
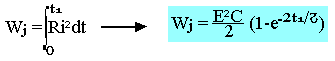
L'énergie électrique emmagasinée en C est:
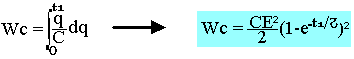
Réponse d'un circuit RL à un échelon de tension
Considérons le circuit suivant:
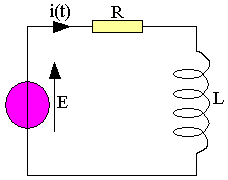
L'excitation a(t) est encore l'échelon de tension et nous nous intéressons à la réponse i(t), intensité du courant parcourant le circuit.
Réponse du circuit.
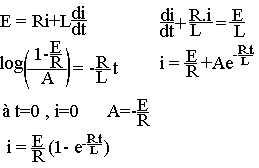
On définit la constante de temps du circuit:
Bilan énergétique
Entre les instants 0 et t1 (t1>0), le générateur fournit l'énergie:
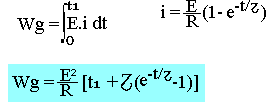
L'énergie dissipée dans R sous forme de chaleur est:
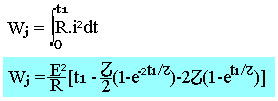
L'énergie électromagnétique emmagasinée dans la bobine L est:
Réponse d'un circuit RLC à un échelon de tension
Considérons le circuit suivant:
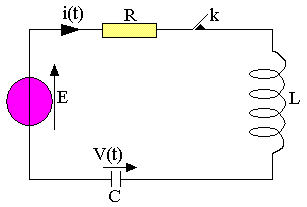
A l'instant t=0 on ferme l'interrupteur K et on étudie la réponse v(t) aux bornes du condensateur C du circuit.
Réponse du circuit
On peut écrire l'équation différentielle du circuit:
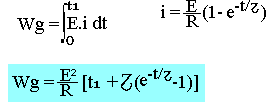
La solution générale de cette équation avec second membre est la somme de l'équation sans second membre et de la solution particulière avec second membre. Cette solution particulière est telle que v=at+b ; v'=a ; V"=0
Recherchons maintenant la forme des solutions de l'équation sans second membre:
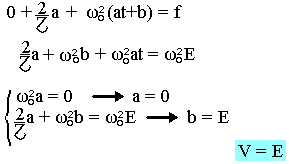
Les solutions de l'équation caractéristiques sont:
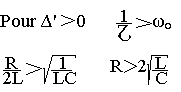
La solution générale de l'équation sans second membre est:
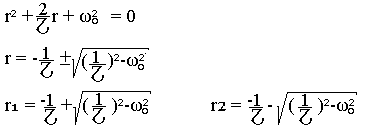
La solution générale de l'équation avec second membre est:
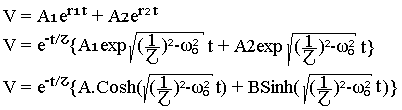
RC est la résistance critique.
La solution générale de l'équation sans second membre est alors:
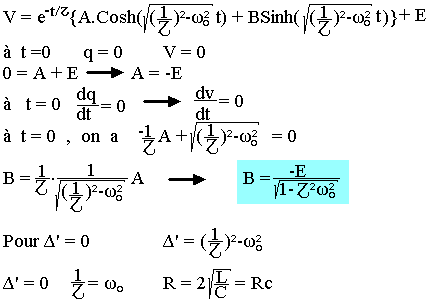
La solution générale de l'équation avec second membre s'écrit:
La solution générale de l'équation sans second membre est:
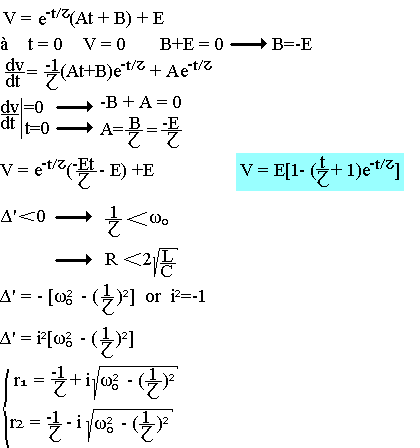
La solution générale de l'équation avec second membre est:
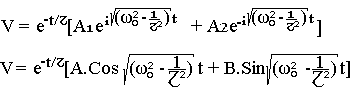
La solution générale avec second membre est:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale