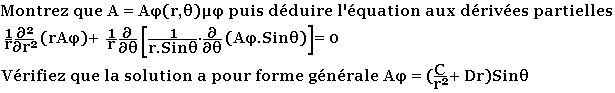Rappels mathématiques: notion d'analyse vectorielle

Notion de champ

Un champ est une application de Rⁿ⟶Rⁿ telle que à tout point de l'espace de dimension m on associe u vecteur de dimension n.
Exemple de champs classiques:

Opération d'analyse vectorielle

Ces opérations ne sont définies qu'en dimension 3

Le gradient

Soit Þ un champ scalaire de R³⟶R, le gradient est une application de l'espace des champs scalaires vers l'espace des champs scalaires vers l'espace des champs vectoriels.

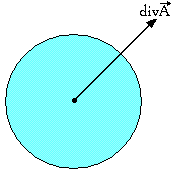
Divergence

Dans cette relation V est un volume fermé et S la surface qui entoure le volume. On peut remarquer que la divergence n'est rien d'autre qu'un sortant d'un volume infinitésimal.

Le champ rotationnel

Le champ rotationnel est une application de l'ensemble des champs vectoriels vers lui-même.
La définition du rotationnel se fait composant par composant c'est-à-dire dans une direction donnée. Si cette direction est le vecteur orienté normal sur A la surface S orientée est donnée par cette relation:

Le rotationnel n'est rien d'autre que la circulation au tour d'une courbe fermée sur un point.

Le Laplacien scalaire

Le Laplacien scalaire est une application de l'ensemble des champs scalaires vers lui-même. Si V est un potentiel, le Laplacien de V se note:

Le Laplacien vectoriel

Le Laplacien vectoriel est une application de l'ensemble des champs vectoriels vers lui-même. Si A est un champ vectoriel:

 

 

---

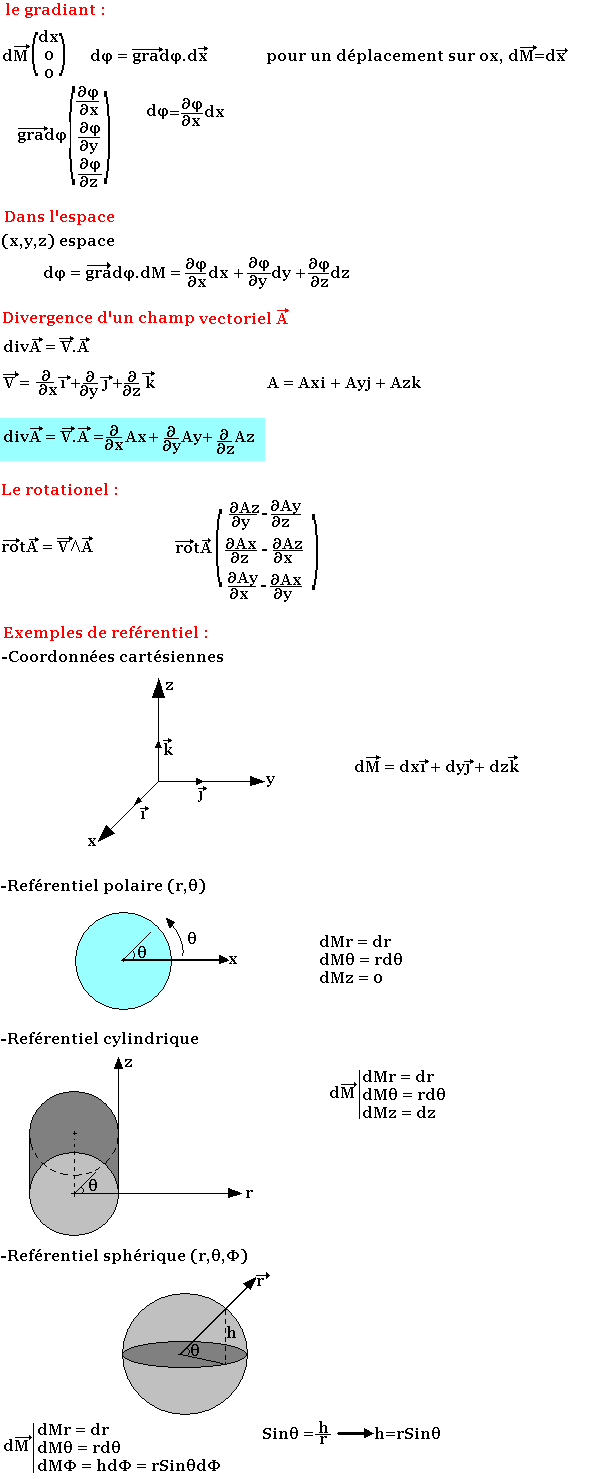
Expression des opérateurs vectoriels en cartésien

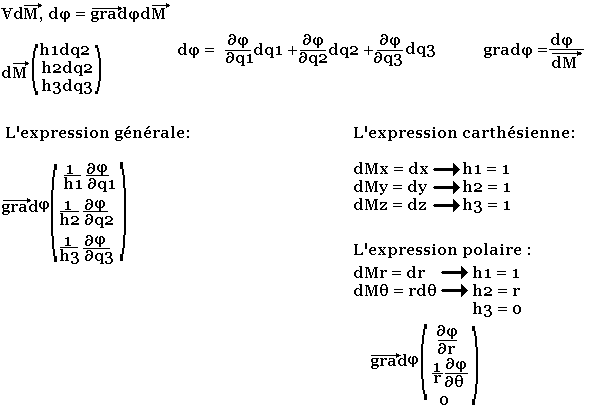
Notion de facteur d'échelle

Dans un référentiel totalement orthogonal, la variation i^ieme composante dqi engendre dans l'espace un déplacement élémentaire dMi=hidqi; le scalaire hi s'appelle facteur d'échelle associé qi. On en déduit les expressions généralisées suivantes quelques soit le référentiel.

Propriétés remarquables

 

 

---

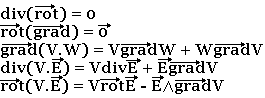
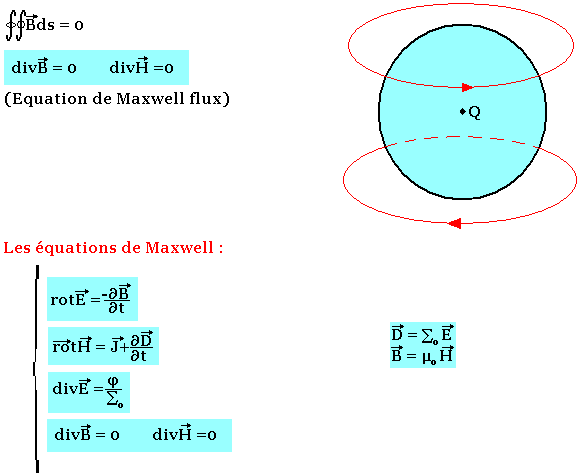
Les équations de Maxwell

Maxwell a élaboré la remarquable théorie électromagnétique de la lumière, ouvrant ainsi la voie sans le savoir aux futures découvertes d'Einstein. En 1873 il a énoncé les équations résumant l'ensemble des phénomènes électromagnétique connes sur le nom d'équation de Maxwell.

Première équation

Appelons B l'induction magnétique à travers un circuit c et dS un élément infinitésimal orienté de la surface S. Le flux magnétique à travers ds est:

D'après la loi de l'induction toute variation de flux de l'induction B à travers un circuit entraine l'existence d'un champ électrique E qui mobilise les électrons d'où la première loi reliant E à B:

Deuxième équation

Un courant électrique d'intensité I et de densité J engendre un champ d'induction magnétique

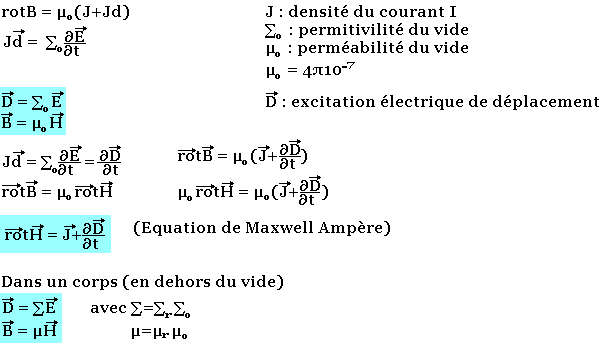
Troisième équation

La présence d'une charge Q dans l'espace entraine la création d'un champ électrique. Le théorème de GAUSS nous dit que le flux sortant d'une surface fermée est égal à la charge intérieure.

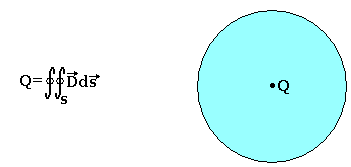
qui n'est rien d'autre que la mesure de la divergence.
Si Þ: charge volumique

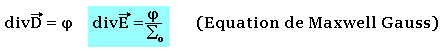
Quatrième équation

Dans un volume donné les lignes de champ magnétiques se referment toujours, la différence entre tout ce qui sort et qui entre dans le volume est toujours nulle.

---

Quelques exercices

Exercice1

Un barreau cylindrique de rayon a de très grande longueur est aimanté uniformément et perpendiculaire à son axe OZ.

Exercice2

Une sphère homogène de rayon a possède une alimentation uniforme M=MU_z, l'origine des coordonnées est choisie au centre de la sphère et on utilise les coordonnées sphériques (r,o,φ).
On se propose de calculer en tout point intérieur et extérieur le potentiel vectoriel A et 'induction magnétique B.