Généralités

Les transistors sont les dispositifs électriques pouvant remplir les fonctions d'amplificateur, de commutation ou d'oscillateur dans les télécommunications, le contrôle et les systèmes informatiques.
Il s sont constitués de minuscules éléments semi-conducteurs généralement du germanium ou du silicium sur lesquels sont effectuées au moins 3 connexions électriques.
On distingue généralement trois grands groupes de transistor:

---

Les transistors à jonction

Structure

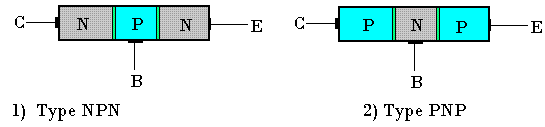
Les transistors à jonction ou transistor bipolaires sont constitués d'un petit monocristal de silicium (une puce, pastille) comportant trois zones dopées successivement NPN ou PNP donc présentant deux jonctions PN de sens opposé:

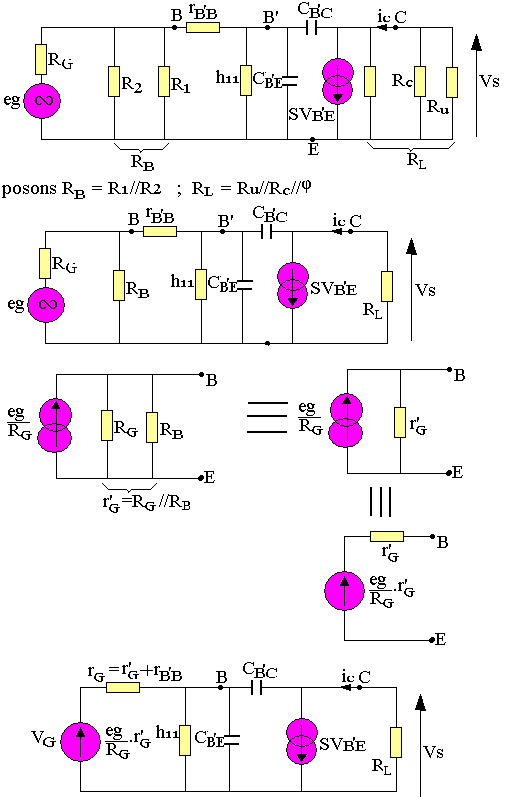
Effet des condensateurs de couplage et de découplage

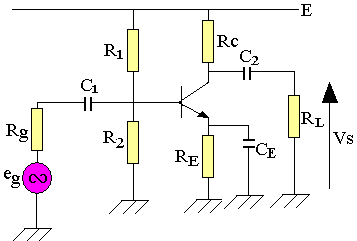
Dans les étages antérieures des montages amplificateurs, on a toujours supposé que les condensateurs de couplage C₁ et C₂ et de découplage C_E étaient des courts-circuits en régime dynamique.
Il n'en est rien car leur impédance 1/jCω a des effets sur le gain des montages.

Effet des condensateurs de couplage

Soit le montage ci-dessous où l'on suppose que seul C_E est un court-circuit en régime dynamique:

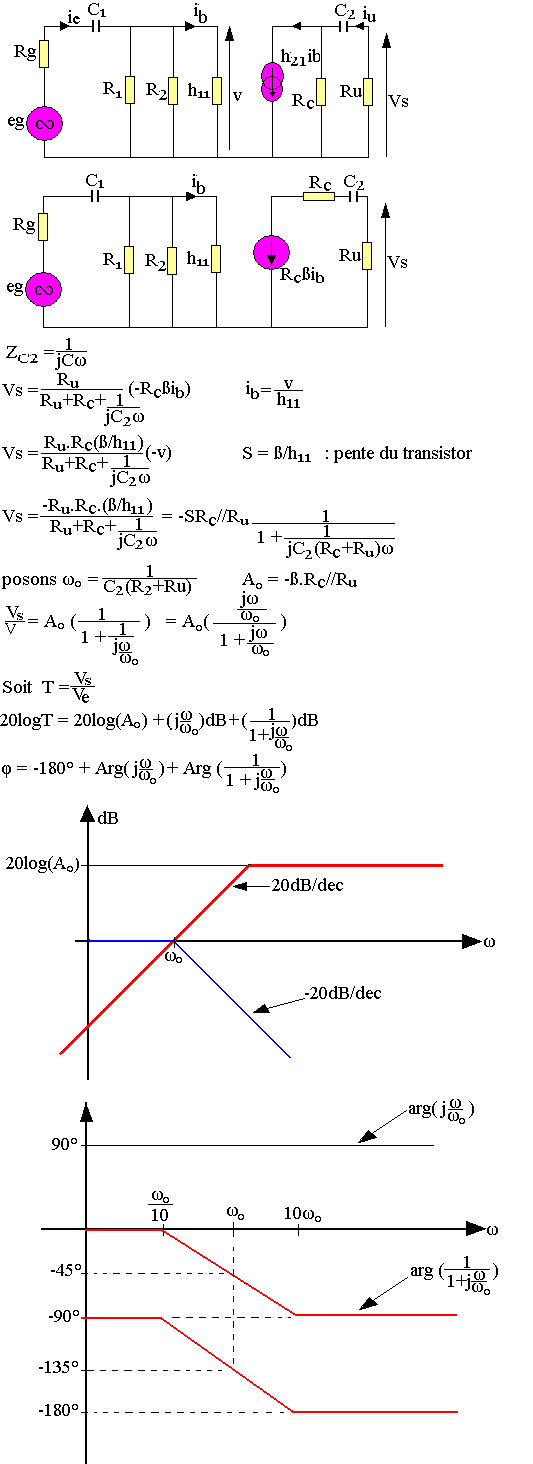
La fréquence de coupure (pulsation) de coupure est la fréquence pour laquelle

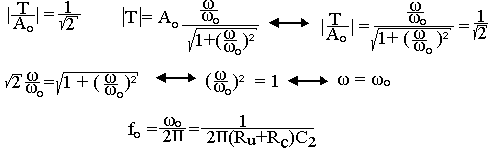
Le gain de l'étage diminue pour tout signal donc la fréquence est inférieure à f₀.

Effet des condensateurs de découplage

Supposons que C₁ et C₂ sont des courts-circuits:

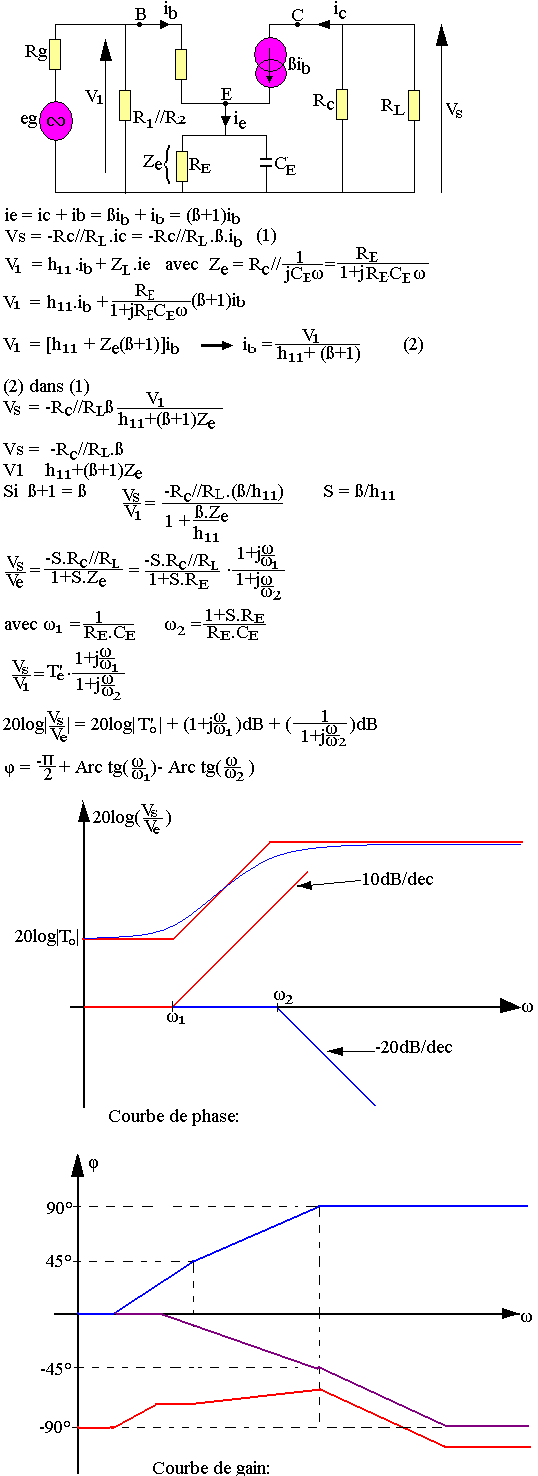
NB: En pratique ω₁<<ω₂

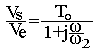
Dans les deux cas nous constatons que le module de la fonction de transfert diminue avec la fréquence. Cela provoque une distorsion du signal est maximale pour une fréquence minimale f_min du spectre du signal. Elle ne doit jamais dépasser 10 à 30%.

 

---

Fonctionnement en haute fréquence

Schéma équivalent

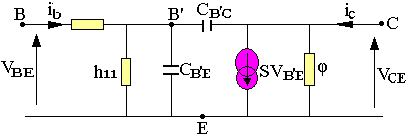
C'est le schéma équivalent de GIOCOLLETTO, c'est le même que celui du transistor en base fréquence complété de trois éléments C_B'E, C_B'C et r_BB'.
C_B'E est la capacité de la jonction d'émetteur.
C_B'C est la capacité de la jonction de collecteur.
r_BB' est la capacité de base ou de volume entre électrode B et le point interne B' se trouvant à la limite de la jonction de l'émetteur.
A cause de la présence des capacités, les courants et les tensions deviennent complexes, le coefficient ß aussi son module |ß| diminue avec l'accroissement de la fréquence. La fréquence pour laquelle ß=1 est appelée fréquence de transition du transistor f_t, elle est donnée par la cathode des transistors.
Le schéma équivalent de GIOCOLLETTO est valable pour les fréquences f<f_t.

Etude du montage émetteur commun à résistance d'émetteur en haute fréquence

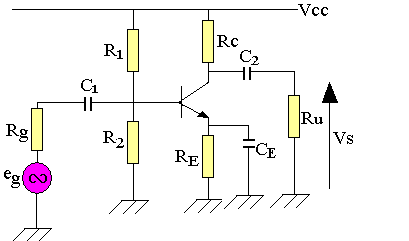
Supposons que C₁, C₂ et C_E sont des courts-circuits.

Théorème de MILLER:

Ce théorème a été proposé pour faciliter l'analyse des amplificateurs en haute fréquence, qui postule que:
Soit deux quadripôles:

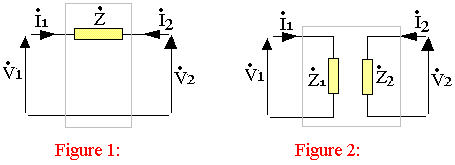
MILLER dit que le quadripôle de la figure1 peut être remplacée par le quadripôle de la figure2 à condition que:

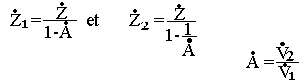
Grâce à ce théorème posons:

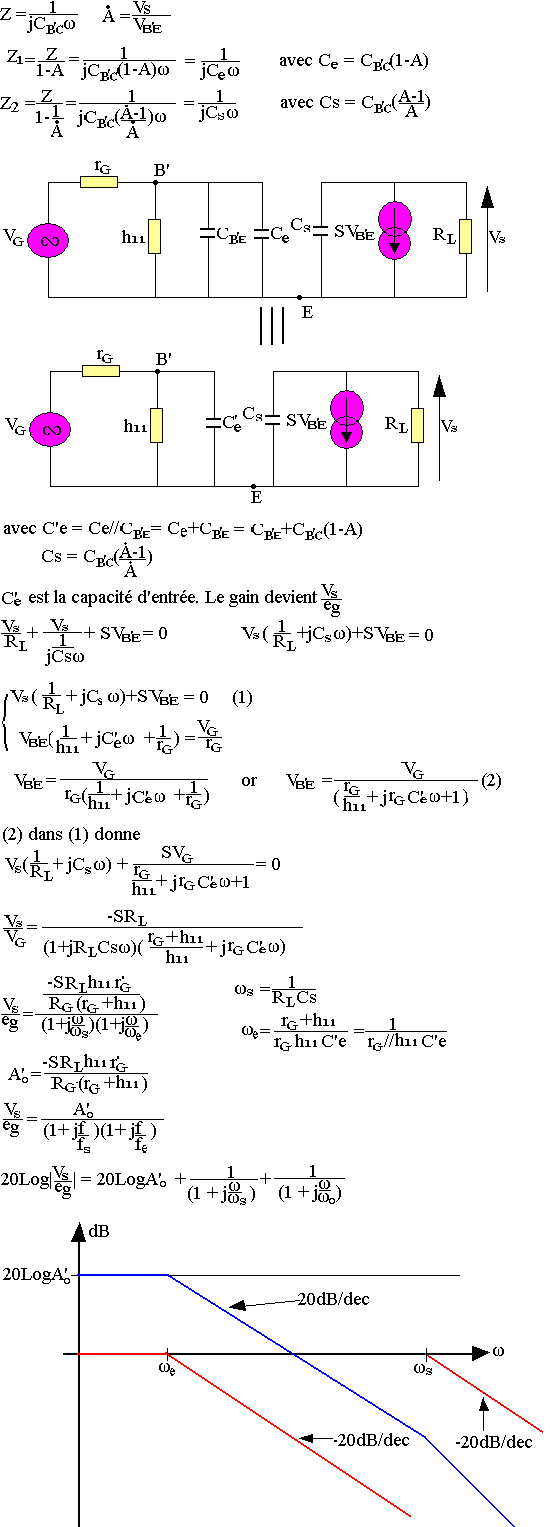
Le gain de l'étage diminue en haute fréquence, il peut même devenir instable car un circuit qui a 2 pôles peut osciller si le gain haute fréquence des deux pôles est supérieure à l'unité.
L'analyse des autres montages (base commune, collecteur commun) donne des résultats presque analogues à celui-ci.

 

---

Amplificateur de puissance

Les derniers étages d'un amplificateur doivent amplifier le courant au lieu de la tension. Pour cela leur courant collecteur se doivent d'être plus grand parce que les résistances de charge sont plis petites, exemple: l'impédance d'un haut parleur vaut 45Ω. Généralement on utilise les transistors en petits signaux à l'entrée des systèmes parce que le signal est faible et les transistors de puissance à la sortie parce que le signal est déjà grand.

Droite de charge statique et dynamique

Tout amplificateur a deux charges: une charge statique (courant continu), une charge dynamique (courant alternatif). Ce qui correspond à deux droite de charge: une statique et l'autre dynamique.

Exemple: Amplificateur émetteur commun.

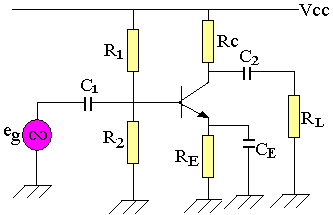
Le schéma équivalent en continu (DC) est:

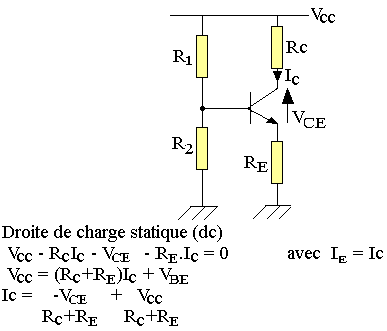
Posons R_dc=R_C+R_E
C'est la résistance de champ statique.
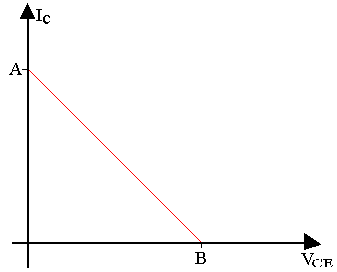
Pour V_CE=0 I_C=V_CC/R_dc
A(0; V_CC/R_dc) : C'est le point de saturation statique.
Pour I_C=0 V_CE=V_CC
B(V_CC; 0) : C'est le point de blocage statique.

Le schéma équivalent en dynamique sera:

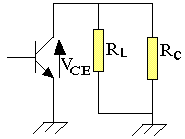
Equation de charge en dynamique
V_CE=-R_C//R_L.i_C
Posons R_ac=R_C//R_L : C'est la résistance de charge dynamique.
i_C = -V_CE/R_ac
La droite de charge dynamique s'écrit i_c=-V_CE/R_ac+b
Pour déterminer b, il suffit de savoir que cette droite passe par le point de repos Q(V_CEQ;I_CQ)
Si I_C=-V_CE/R_ac+b passe par Q I_CQ=-V_CEQ/R_ac+b b=I_CQ+V_CEQ/R_ac
D'où l'équation de la droite de charge est: i_C=-V_CE/R_ac+I_CQ+V_CEQ/R_ac
Pour V_CE=0 I_C=I_CQ+V_CEQ/R_ac
A'(0; I_CQ+V_CEQ/R_ac) pour I_C=0 V_CE=R_acI_CQ+V_CEQ
B'(R_acI_CQ+V_CEQ; 0)

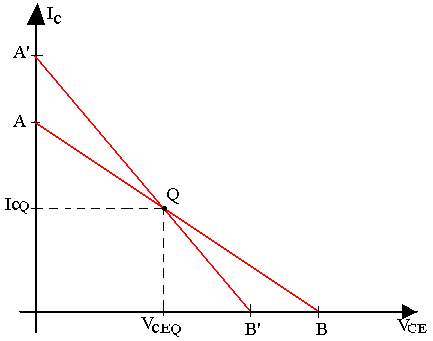
En l'absence du signal le transistor est au point Q appelé point de repos.
En présence d'un signal le point de fonctionnement dévie sur la droite de charge dynamique plutôt que sur la droite de charge statique.
Cette droite est dite dynamique parce qu'elle se représente tous les points de fonctionnement dynamique du transistor.

Dynamique du signal de sortie

Durant l'alternance positive du signal d’entrée, la tension du collecteur varie du point Q vers le point de saturation dynamique, tandis que durant l'alternance négative, la tension collecteur varie du point Q vers le point de blocage dynamique.
La dynamique du signal de sortie est la tension alternative de crête à crête non écrêtée maximale qu'un amplificateur peut produire.
L'excursion positive maximale de la tension de sortie à partir du point Q est V₁-VCESat

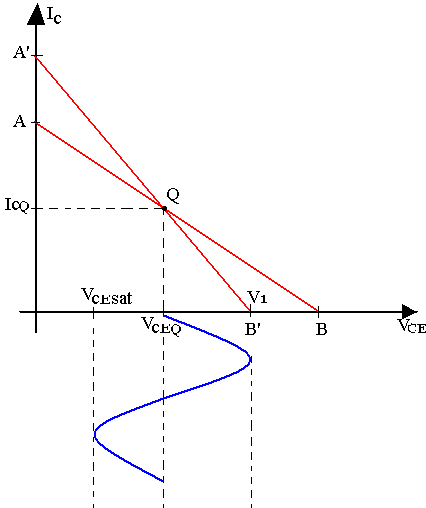
Si nous désignons par PP la dynamique du signal de sortie d'un amplificateur émetteur commun, elle sera égale à la plus petite des deux variables suivantes:
PP = 2R_acI_CQ
PP = 2(V_CEQ-V_CESat) = 2V_CEQ
Pour un amplificateur de grand signaux ou alors pour qu'un amplificateur de puissance puisse avoir une dynamique maximale du signal de sortie, il convient de placer le point Q au milieu de la droite de charge dynamique. Dans ces conditions (C'est-à-dire celle d'une dynamique maximale du signal de sortie) on peut écrire que 2R_acI_CQ=V_CEQ ↔ R_acI_CQ=V_CEQ
Dans ces cas au point de repos Q l'équation de la droite de charge statique donne:
I_CQ=-V_CEQ/R_ac+V_CC/R_dc or V_CEQ=R_acI_CQ I_CQ=-R_acI_CQ/R_dc+V_CC/R_dc
I_CQ = V_CC/R_dc(1+Rac/R_dc) = V_CC/(R_dc+R_ac)
V_CEQ=R_acI_C=R_ac[V_CC/(R_dc+R_ac)]
V_CEQ = V_CC/(1+R_dc/R_ac)

Exercice d'application

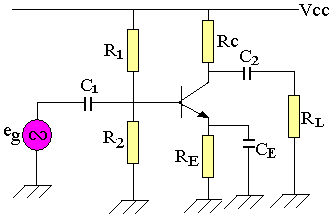
Equation de la droite de charge
V_CC=(R₄+R₃)I_C+V_CE ; I_C=I_E
I_C = V_CC/(R₄+R₃) - V_CE/(R₄+R₃)
I_C = -V_CE/R_dc + V_CC/R_dc = -0,217V_CE+2,6 (mA)
Si I_C=0 ; V_CE=V_CC alors B(V_CC;0)=(12;0)
Si V_CE=0 ; I_C=V_CE/R_dc alors A(0;V_CC/R_dc)=(0; 2,6)

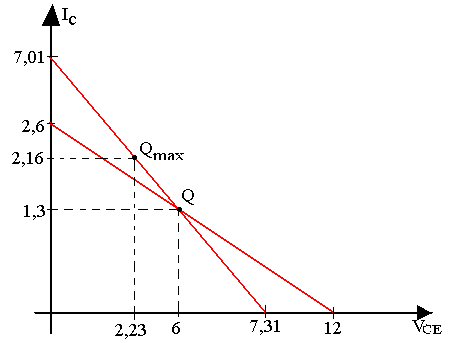
On admet que le point de repos se trouve au milieu de la droite de charge statique.

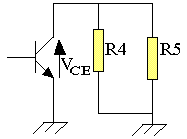
V_CE=-R₄//R₅i_C
i_C=-V_CE/(R₄//R₅)+b
Q(12/2; 26/2) = (6; 1,3) cette droite passe par Q
1,3=-6/(R₄//R₅)+b or R₄//R₅=1,05KΩ

b=1,3+6/1,05 = 1,3+5,71 = 7,01 mA
i_C = -V_CE/1,05+7,01 mA
i_c = -0,95V_CE+7,01 mA
A'(0; 7,01)mA et B(7,37; 0)
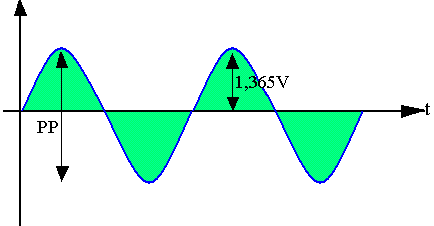
Déterminons la dynamique de sorti
PP = inf{2.R_acI_CQ ; 2(V_CEQ-V_CESat)}
PP = inf { 2.1,05x10³.1,3x10^-3=2,73 ; 2(6-0)=12}
PP = 2,73
Tension max aux bornes de la charge PP/2 = 1,365V

Déterminez les coordonnées du point de repos correspondant à une dynamique maximale du signal de sortie.
I_CQ=V_CC/(R_ac+R_dc) = 12/(1,05+4,5) = 2,16mA
V_CEQ=V_CC/(1+R_dc/R_ac) = 12/(1+4,6/1,05) = 2,23V
I_CQ = 2,16mA et V_CEQ = 2,23V
Dans ce cas la dynamique maximale de sortie sera de 4,46V et l'amplitude V_S=2,23V

Droite de charge des autres montages

Amplificateur à collecteur commun

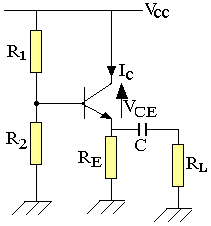
V_CC=R_EI_C+V_CE
I_C=-V_CE/R_E+V_CC/R_E
R_dc=R_E
En alternatif on a:

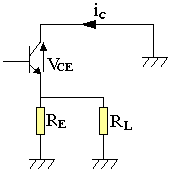
V_CE=-R_E//R_Li_C
R_ac=R_E//R_L
PP = 2V_CEQ
PP = 2R_acI_CQ

Amplificateur stabilisé

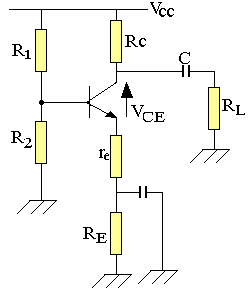
Droite de charge statique:
V_CC=(R_C+r_e+R_e)I_C+V_CE
R_dc=R_C+r_e+R_E
Droite de charge en alternatif:

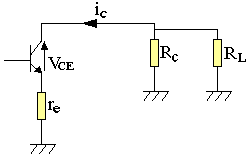
i_e(R_C//R_L+r_e)=v_CE
R_ac=r_e+R_C//R_L
PP = 2R_E//R_LI_CQ
PP = 2V_CEQ(R_C//R_L)/(R_L//R_C//R_L+r_e)