Les transistors - Exercice d'application

Exercice d'application

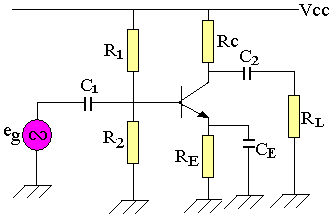
Equation de la droite de charge
V_CC=(R₄+R₃)I_C+V_CE ; I_C=I_E
I_C = V_CC/(R₄+R₃) - V_CE/(R₄+R₃)
I_C = -V_CE/R_dc + V_CC/R_dc = -0,217V_CE+2,6 (mA)
Si I_C=0 ; V_CE=V_CC alors B(V_CC;0)=(12;0)
Si V_CE=0 ; I_C=V_CE/R_dc alors A(0;V_CC/R_dc)=(0; 2,6)

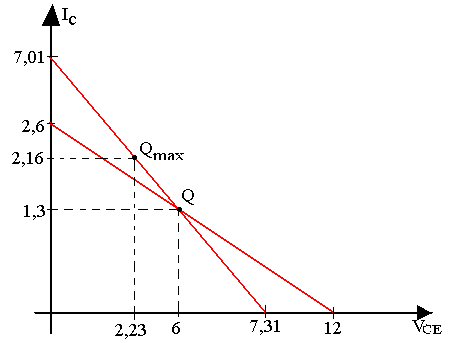
On admet que le point de repos se trouve au milieu de la droite de charge statique.

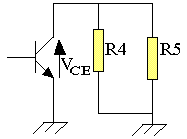
V_CE=-R₄//R₅i_C
i_C=-V_CE/(R₄//R₅)+b
Q(12/2; 26/2) = (6; 1,3) cette droite passe par Q
1,3=-6/(R₄//R₅)+b or R₄//R₅=1,05KΩ

b=1,3+6/1,05 = 1,3+5,71 = 7,01 mA
i_C = -V_CE/1,05+7,01 mA
i_c = -0,95V_CE+7,01 mA
A'(0; 7,01)mA et B(7,37; 0)
Déterminons la dynamique de sorti
PP = inf{2.R_acI_CQ ; 2(V_CEQ-V_CESat)}
PP = inf { 2.1,05x10³.1,3x10^-3=2,73 ; 2(6-0)=12}
PP = 2,73
Tension max aux bornes de la charge PP/2 = 1,365V

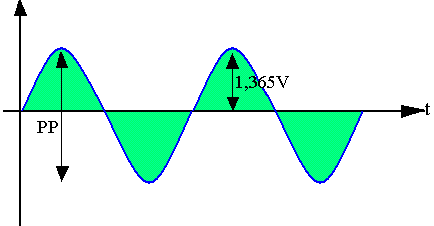
Déterminez les coordonnées du point de repos correspondant à une dynamique maximale du signal de sortie.
I_CQ=V_CC/(R_ac+R_dc) = 12/(1,05+4,5) = 2,16mA
V_CEQ=V_CC/(1+R_dc/R_ac) = 12/(1+4,6/1,05) = 2,23V
I_CQ = 2,16mA et V_CEQ = 2,23V
Dans ce cas la dynamique maximale de sortie sera de 4,46V et l'amplitude V_S=2,23V

Droite de charge des autres montages

Amplificateur à collecteur commun

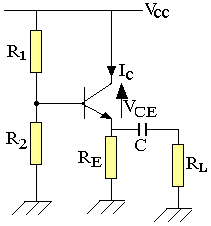
V_CC=R_EI_C+V_CE
I_C=-V_CE/R_E+V_CC/R_E
R_dc=R_E
En alternatif on a:

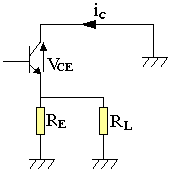
V_CE=-R_E//R_Li_C
R_ac=R_E//R_L
PP = 2V_CEQ
PP = 2R_acI_CQ

Amplificateur stabilisé

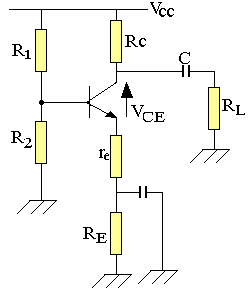
Droite de charge statique:
V_CC=(R_C+r_e+R_e)I_C+V_CE
R_dc=R_C+r_e+R_E
Droite de charge en alternatif:

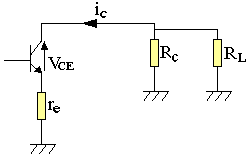
i_e(R_C//R_L+r_e)=v_CE
R_ac=r_e+R_C//R_L
PP = 2R_E//R_LI_CQ
PP = 2V_CEQ(R_C//R_L)/(R_L//R_C//R_L+r_e)