Fonctions numériques

Généralités

Ensemble de définition

Soit f une fonction de E → F, on appelle ensemble de définition de f noté D_f l'ensemble constituant les éléments de E qui ont une image dans F.

Exemple:

Calcul le domaine de définition de la fonction suivante:

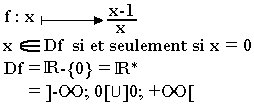
Le domaine de définition d'une fonction se donne nécessairement sous forme d'intervalle et de réunion d'intervalle.

Ensemble le de définition des fonctions usuelles

Fonction polynôme

Ce sont des fonctions du type f(x)=a_px^p+a_p-1x^p-1+...+a₀

Théorème:

Toute fonction polynôme f a pour ensemble de définition D_f=IR=]-∞; ∞+ [

Fonction homographique

Ce sont des fonctions du type:

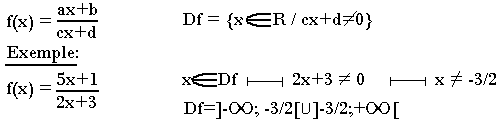
Une fonction homographique est un cas particulier de fonction rationnelle.

Cas des fonctions rationnelles

Ce sont des fonctions de la forme h(x)=h(x)/g(x).
f(x) et g(x) étant des fonctions polynômes
D_h={x appartenant à R / g(x) différent de 0}

Fonctions irrationnelles

Ce sont des fonctions de la forme suivante: