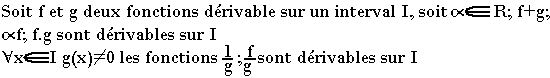Dérivabilité d'une fonction

Soit x_o appartenant à R, soit f:R → R, f est dérivable en x_o si et seulement si

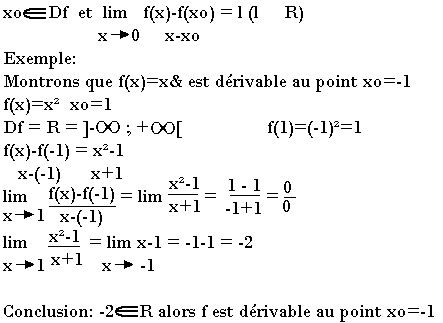
Remarque:

Cette limite l=f'(x_o) est appelée nombre dérivée.

Théorème:

Toute fonction dérivable en un point x_o est continue en x_o. Mais la réciproque n'est pas toujours vérifiée.

Dérivabilité à gauche ; dérivabilité à droite

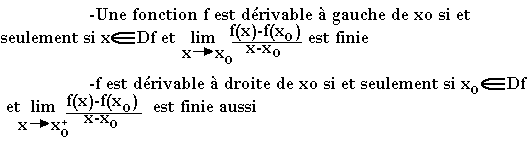
Théorème:

f est dérivable au point x_o si et seulement si f est dérivable à gauche de x_o et dérivable à droite de x_o

Dérivabilité sur un intervalle

Une fonction f est dérivable sur un intervalle I si et seulement si elle est dérivable en tout point de I

Théorème:

Toute fonction polynôme est dérivable sur R.
Toute fonction rationnelle est dérivable dans son ensemble de définition.

Fonctions dérivables usuelles

Opération sur les fonctions dérivées