Continuité d'une fonction

Soit x_o appartenant à R, soit f une fonction de R→R, f est dite continue au point x_o si et seulement si x_o appartient à D_f et
lim f(x) = f(x_o)
x → x_o

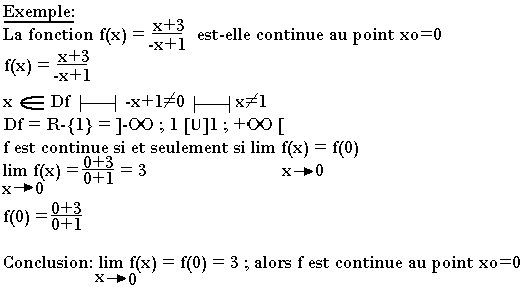
Continuité à gauche ; continuité à droite

Remarque:

f est continue en x_o si et seulement si
lim f(x) = lim f(x)
x → x^-_o x → x⁺_o

Opération sur les fonctions continues

Soit x_o appartient à IR f:IR → IR et g:IR → IR

Prolongement par continuité d'une fonction

Considérons une fonction f définie sur D. La fonction f est définie sur un intervalle de centre x_o mais pas en x_o mais en x_o et admet une limite en x_o. Soit la fonction g telle que:

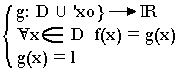
Cette fonction g est continue en x_o car
lim g(x) = g(x_o)
x → x_o
Prolongement de f par continuité en x_o