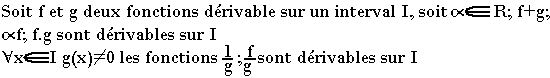Généralités
Ensemble de définition
Soit f une fonction de E → F, on appelle ensemble de définition de f noté Df l'ensemble constituant les éléments de E qui ont une image dans F.
Exemple:
Calcul le domaine de définition de la fonction suivante:
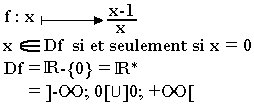
Le domaine de définition d'une fonction se donne nécessairement sous forme d'intervalle et de réunion d'intervalle.
Ensemble le de définition des fonctions usuelles
Fonction polynôme
Ce sont des fonctions du type f(x)=apxp+ap-1xp-1+...+a0
Théorème:
Toute fonction polynôme f a pour ensemble de définition Df=IR=]-∞; ∞+ [
Fonction homographique
Ce sont des fonctions du type:
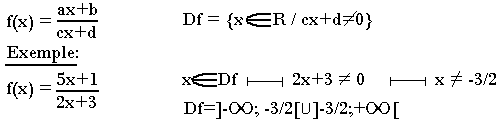
Une fonction homographique est un cas particulier de fonction rationnelle.
Cas des fonctions rationnelles
Ce sont des fonctions de la forme h(x)=h(x)/g(x).
f(x) et g(x) étant des fonctions polynômes
Dh={x appartenant à R / g(x) différent de 0}

Fonctions irrationnelles
Ce sont des fonctions de la forme suivante:
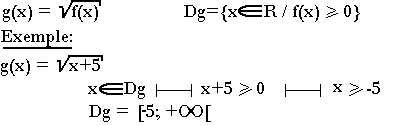
Parité et périodicité
Parité des fonctions
Une fonctions est dite paire si et seulement si
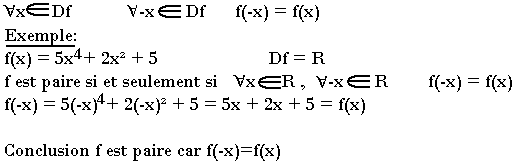
Une fonction est dite impaire si et seulement si
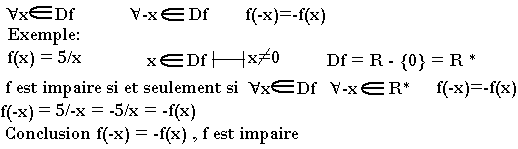
Périodicité
Une fonction f définie sur un intervalle I est périodique s'il existe un nombre réel positif T tel que
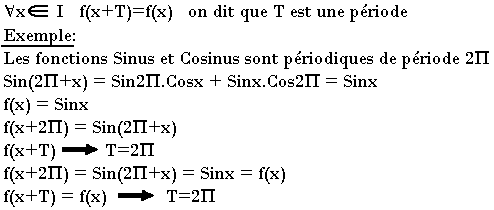
Limite d'une droite
On dit qu'une fonction f a pour limite, le réel l quand x→ x0. Si les valeurs de f(x) peuvent être rendues aussi de l que l'on veut en approchant x et x0 et on note
lim f(x)=l
x→x0
Exemple:
Calculer la limite de la fonction f(x)=7x-2 ; x0=2
![]()
Unicité de la limite
Théorème:
La limite d'une fonction en un point lorsqu'elle existe est unique.
Limite à gauche; limite à droite
- On parle de limite à gauche de xo pour la condition x<x0 et on note:
lim f(x)
x → x-o - Si on pose comme condition x>xo la fonction admet une limite à droite de xo et on note
lim f(x)
x → >xo
ou bien encore
lim f(x)
x → x+o
Théorème:
Une fonction f admet une limite au point xo si et seulement si
lim f(x) = lim f(x)
x → x-o x → x+o
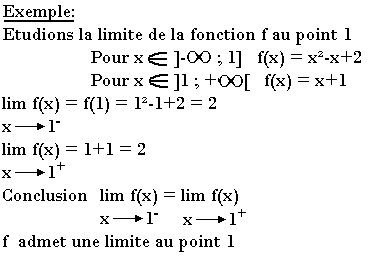
limite en plus l'infinie ou moins l'infinie
f(x) = 1/x
Quand x devient infiniment très grand 1/x devient très petit en se rapprochant de 0, on a alors
![]()
Fonction constante
Si f est une fonction constante f(x)=C, C appartient à R
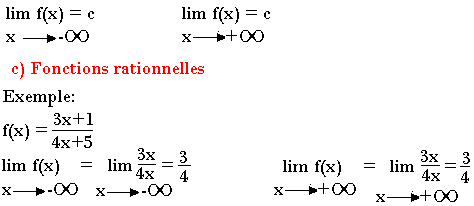
Théorème:
La limite d'une fonction rationnelle à "moins l'infini" ou à "plus l'infini" est égale à la limite du rapport des monômes de plus haut degré.
Limite infinie en xo
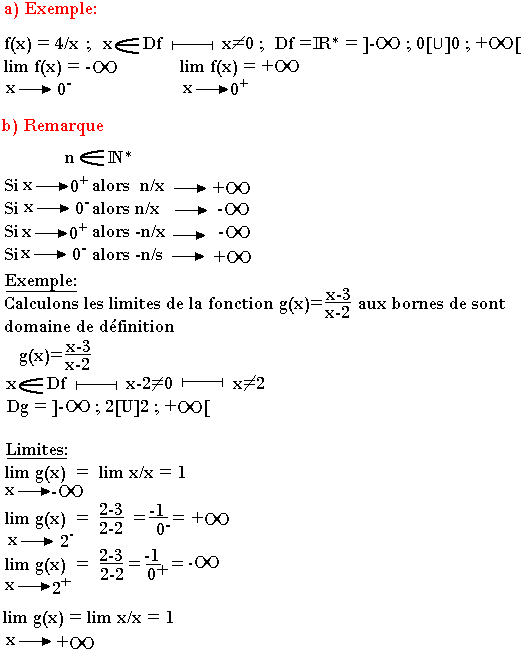
Limite infinie à "plus l'infinie" ou à "moins l'infinie"
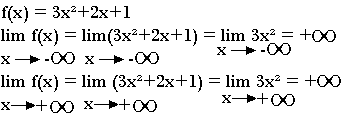
Théorème:
La limite d'une fonction polynôme, lorsque x tant vers plus ou moins l'infinie est égale à la limite du monôme du plus haut degré.
Limite d'une somme d'un produit et d'un rapport de fonction

Les formes indéterminées
Ce sont des formes qui ne demandent pas une conclusion directe et où il faut préalablement lever l'indétermination. On distingue comme forme indéterminée:

Continuité d'une fonction
Soit xo appartenant à R, soit f une fonction de R→R, f est dite continue au point xo si et seulement si xo appartient à Df et
lim f(x) = f(xo)
x → xo
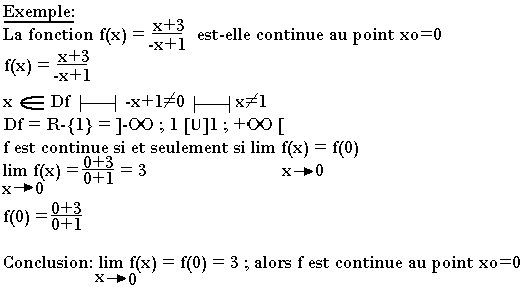
Continuité à gauche ; continuité à droite

Remarque:
f est continue en xo si et seulement si
lim f(x) = lim f(x)
x → x-o x → x+o
Opération sur les fonctions continues
Soit xo appartient à IR f:IR → IR et g:IR → IR
- Si f et g sont continues en xo alors f+g est continues en xo alors f+g est continue en xo
- Si f et g sont continues en xo alors fxg est continues en xo
- Quelque soit x appartenant à R g(x) différent de 0 si f et g sont continues en xo alors f/g est continue en xo
Prolongement par continuité d'une fonction
Considérons une fonction f définie sur D. La fonction f est définie sur un intervalle de centre xo mais pas en xo mais en xo et admet une limite en xo. Soit la fonction g telle que:
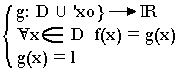
Cette fonction g est continue en xo car
lim g(x) = g(xo)
x → xo
Prolongement de f par continuité en xo
Dérivabilité d'une fonction
Soit xo appartenant à R, soit f:R → R, f est dérivable en xo si et seulement si
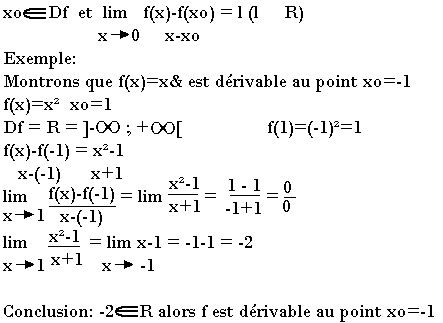
Remarque:
Cette limite l=f'(xo) est appelée nombre dérivée.
Théorème:
Toute fonction dérivable en un point xo est continue en xo. Mais la réciproque n'est pas toujours vérifiée.
Dérivabilité à gauche ; dérivabilité à droite
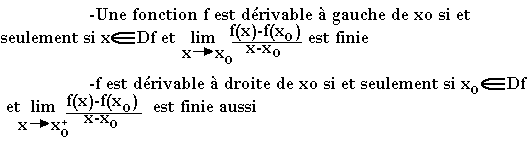
Théorème:
f est dérivable au point xo si et seulement si f est dérivable à gauche de xo et dérivable à droite de xo
Dérivabilité sur un intervalle
Une fonction f est dérivable sur un intervalle I si et seulement si elle est dérivable en tout point de I
Théorème:
Toute fonction polynôme est dérivable sur R.
Toute fonction rationnelle est dérivable dans son ensemble de définition.
Fonctions dérivables usuelles
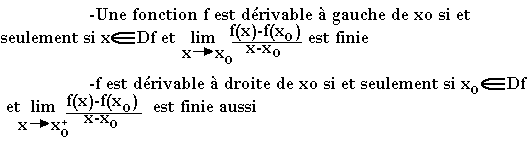
Opération sur les fonctions dérivées