Définitions et généralités
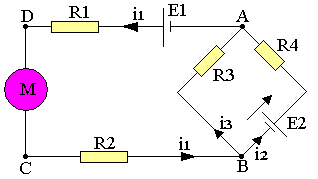
- Un réseau est un ensemble de conducteurs reliés entre eux et contenant en général des générateurs, des récepteurs et des résistances.
- Un noeud est un point du réseau où sont connectés plus de deux conducteurs.
- Une branche est une portion du réseau située entre deux noeuds.
- Une maille est un ensemble de branchement formant un circuit fermé qui ne passe qu'une fois par un noeud donné.
Dans les réseaux, le problème qui se pose est le suivant:
- Les résistances, les forces électromotrices, les forces contre électromotrices étant comme il faut déterminer les intensités des courants qui circulent dans chaque branche en grandeur et en sens
- Il y'a évidemment autant d'inconnue que de branchement que de branche il faut donc trouver les équations en nombre suffisant pour trouver les inconnues.
- Nous allons donc passer en revue les différentes méthodes d'étude et nous mettons chaque fois en relief leur qualité et leur défaut.
Lois de KIRCHOFF
Il en existe deux, celle relative aux noeuds et celle relatives aux maille.
Loi relative aux noeuds
Considérons un noeud A où passent des courants d'intensité i1, i2, i3, i4 et i5
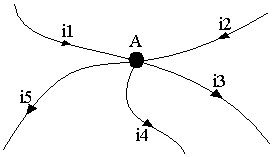
On a alors i1+i2=i3+i4+i5
Ainsi les différents courants entrant et sortant en un noeud sont liais par la relation
Somme de courants entrants = somme de courants sortants.
Loi relative aux mailles
La loi d'Ohm généralisée est valable ici et s'écrit
![]()
En prenant un circuit fermé A B on a:
![]()
La loi KIRCHOFF relative aux mailles s'écrit alors
![]()
Utilisation des lois de KIRCHOFF
Pour utiliser les lois de KIRSHOFF on procède de la manière suivante:
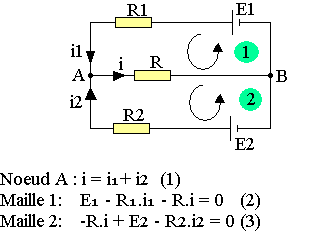
- Sur chaque branche on adapte un sens positif de mesure pour le courant, le plus vraisemblable et une valeur algébrique du courant. On écrit les lois relatives aux noeuds i1=i2+i3au noeud B
- On écrit ensuite la loi relative aux mailles pour le nombre convenables de maille indépendante en prenant sur chaque maille un sens de parcours arbitraire.
- R3i3+R4i2-E2=0
- On obtient ainsi un nombre d'équation linéaire permettant de calculer les intensités inconnues la résolution de ce système d'équation forme les valeurs algébriques des intensités.
Les valeurs positives signifient que le courant circule effectivement dans le sens choisi, s'il y'a pas de récepteur non polarisé, des valeurs négatives signifient que le courant circule dans le sens opposé.
Enfin s'il y'a des récepteurs non polarisés et si l'on trouve dans une branche contenant un tel récepteur une intensité négative, il faut recommencer les calculs en inversant le sens de cette intensité. Le récepteur non polarisé s'opposant toujours à l'intensité.
Si en fin de calcul on trouve dans cette branche une intensité positive tout va bien.
Si on trouve encore une intensité négative, cela signifie que la ddp aux bornes du récepteur est insuffisante pour faire fonctionner celui-ci: aucun courant ne traverse dans la branche et on peut le supprimer.
Le calcul est terminé lorsque toutes les intensités sont positives dans toutes les branches contenant des récepteurs non polarisés.
Exemple
Nous nous proposons d'appliquer les lois de KIRSHOFF au réseau suivant:
Méthode des courants des mailles
Principe
Il ne s'agit pas d'une nouvelle méthode mais d'un moyen systématique de contourner certaines difficultés rencontrées dans la méthode de Kirchhoff. Précisons en particulier que ce moyen rend de précieux services lorsque le réseau présente un grand nombre de maille. La méthode réside dans un chargement de variable.
- On intègre que les petites mailles indépendantes sont parcourues toutes dans le même sens par les courants noté j1, j2, ..., jn
- On écrit les équations de Kirchhoff relatives aux mailles.
- On calcule les courants fictifs des mailles indépendantes et on déduit les courants réels de branche
Exemple
On considère le circuit suivant dont on se propos de calculer les intensités dans les différentes branches par la méthode des mailles fictives.
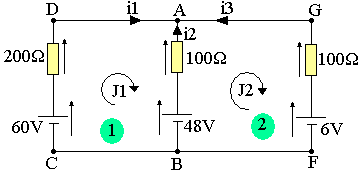
- Une branche telle que CD appartient uniquement à la maille ABCDA donc i1=J1 ; i3=J2
- Une branche telle que AB appartient aux mailles ABCDA et ABFGA, alors vue de (1) et J2-J1, vue de (2)
- maille (1)
-200J1 - 100(J1-J2) - 48 + 60 = 0
-200J1 - 100J1 + 100J2 = -12
maille (2)
100J2 - 6 + 48 + 100(J2-J1) = 0
J1=0,132A ; J2=0,276A
i1 = J1 = 0,132A
i3 = -J2 = -0,276A
i2 = i1 + i3 = 0,144A
On considère le circuit suivant
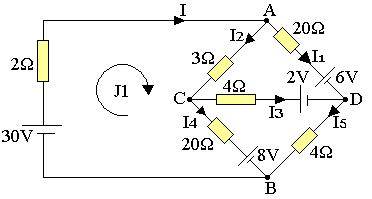
Loi des noeuds:
noeud A: I=I1+I2
noeud B: I=I4+I5
noeud C: I2=I4+I3
noeud D: I5=I1+I3
Loi des mailles
maille (1):
-30 + 2J1 + 3(J1-J2) + 20(J1-J3) + 8 = 0
25J1 - 3J2 - 20J3 = 22
maille (2):
20J2 + 6 - 2 + 4(J2-J3 + 3(J2-J1) = 0
-3J1 + 27J2 - 4J3 = -4
maille (3):
4J3 - 8 + 20(J3-J1) + 4(J3-J2) + 2 =0
-20J1 - 4J2 + 28J3 = 6
Théorèmes de Thevenin et de Norton
Les théorèmes de Thevenin et de Norton permettent de modifier des portions de circuits afin de calculer les intensités et les tensions dans des branches déterminées.
Théorème de Thevenin
Un dipôle actif est équivalent vu de ses deux bornes à un générateur de tension, donc:
- La force électromotrice est la différence de potentielle aux bornes du dipôle en circuit ouvert.
- La résistance interne est la résistance équivalente vue des deux bornes du dipôle, lorsqu'on a enlevé toutes les forces électromotrices tout en gardant les résistances.
Ce générateur équivalent est dit générateur de Thevenin.
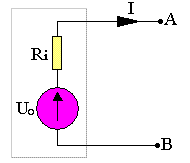
On a VA-VB=U0-RiI
Ainsi on note Eth la f.e.m du générateur de Thevenin et Rth sa résistance interne telle que Eth=U0, Rth=Ri
Exemple:
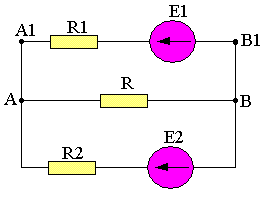
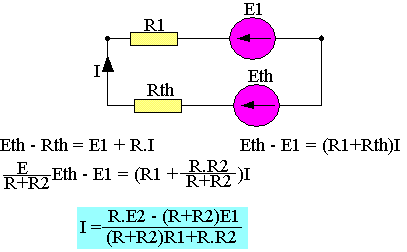
Nous nous proposons de calculer au moyen du théorème de Thevenin l'intensité traversant le dipôle (E1, R1). Il nous faut donc modifier le dipôle A1E2B1
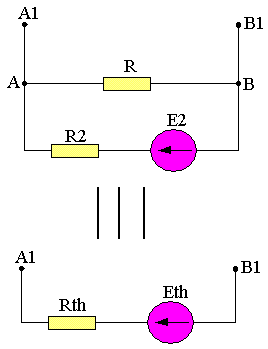
VA-VB=RI2=E2-R2I2=U0
I2=U0/R ; Eth=R.E2/(R+R2)
1/Rth=1/R+1/R2 ; Rth=R.R2/(R+R2)
Théorème de Norton
Ce théorème nous donne une autre modélisation d'un dipôle actif. Schématisons à nouveau le dipôle actif par un générateur de Thevenin, puis établissons un court-circuit entre les bornes A et B
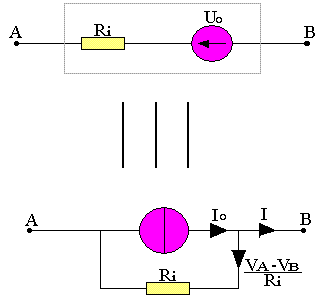
Le dipôle est traversé par un courant d'intensité I0 tel que I0=U0/Ri.
Or VA-VB=U0-RiI=U0-(VA-VB)
I=U0/Ri-(VA-VB)/Ri
I=I0-(VA-VB)/Ri
Théorème:
Un dipôle est équivalent, vu de ses deux bornes à un générateur de courant donc:
- Le courant principal I0 est le courant de court-circuit du dipôle.
- La résistance interne montée en parallèle est la résistance équivalente vue des bornes du dipôle lorsqu'on a enlevé toutes les forces électriques. Cette résistance débite un courant (VA-VB)/Ri
Application du théorème de Thevenin pour le calcul de la tension dans une branche
On considère le réseau suivant en nous proposant de calculer la différence de potentielle entre le point A et B.
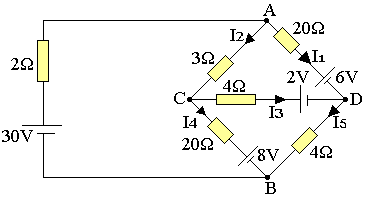
On supprime la dite branche et on écrit:
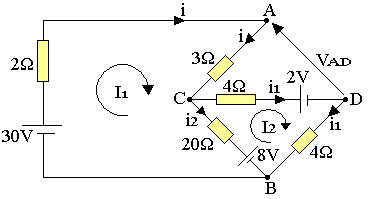
VA-VD=(VA-VC)+(VC-VB)+(VB-VD)=3i-4i1+8+20i2
Déterminons i, i1 et i2
(1): -30+2I1+3I1+20(I1-I2)+8=0 ↔ 25I1-20I2=22
(2): 4I2 +2+4I2-8+20(I2-I1)=0 ↔ -20I1+28I2=6
I1=2,45A ; I2=1,96A
i=I1=2,45A
i1=I2=1,96A
i2=i-i1=2,45-1,96=0,48A
VA-VD=3x2,45-4x1,96+20x0,48+8
VA-VB=17,11V
Théorème de Milmann
Principe
Considérons la portion de circuit suivante:
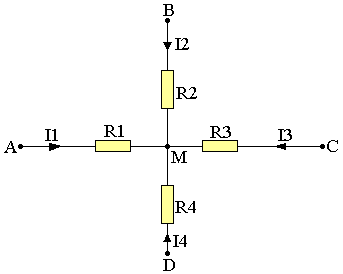
Au noeud M on peut écrire I1+I2+I3+I4=0
or VA-VM=R1I1
VB-VN=R2I2
VC-VM=R3I3
VD-VM=R4I4
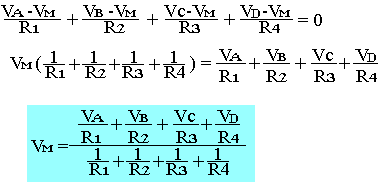
Théorème
Soit un certain nombre de branche se rejoignant au point M.
Soit Ri les résistances de chacun de ces branches et Vi le potentiel à l'extrémité de chaque branche. On peut écrire:
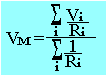
Exemple
On considère à nouveau le circuit suivant:
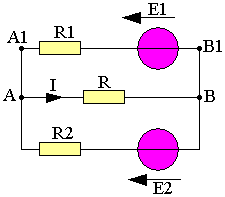
On peut écrire au noeud A
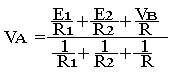
En prenant comme origine potentielle VB=0
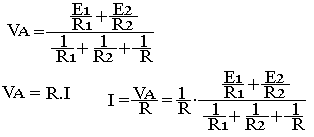
Transformation de KENELLY
Lorsqu'on fait l'étude d'un réseau électrique, il est souvent nécessaire de remplacer trois résistances branchées en triangle par trois résistances branchées en étoile et choisir de telle sorte que les deux montages soient équivalent, c'est-à-dire que le fonctionnement du reste du réseau ne soit pas perturbé par la substitution. La transformation inverse est quelquefois intéressante.
Passage du triangle à l'étoile
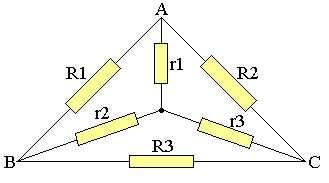
Supposons que l'on coupe la connexion du réseau des résistances avec le reste du réseau dans C.

Passage de l'étoile au triangle
Il suffit d'extraire les expressions de R1, R2, R3 des relations générales précédentes. Pour cela calculons les expressions r1r2+r2r3+r3r1

