Théorèmes de Thevenin et de Norton
Les théorèmes de Thevenin et de Norton permettent de modifier des portions de circuits afin de calculer les intensités et les tensions dans des branches déterminées.
Théorème de Thevenin
Un dipôle actif est équivalent vu de ses deux bornes à un générateur de tension, donc:
- La force électromotrice est la différence de potentielle aux bornes du dipôle en circuit ouvert.
- La résistance interne est la résistance équivalente vue des deux bornes du dipôle, lorsqu'on a enlevé toutes les forces électromotrices tout en gardant les résistances.
Ce générateur équivalent est dit générateur de Thevenin.
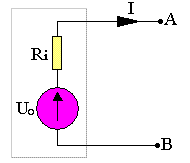
On a VA-VB=U0-RiI
Ainsi on note Eth la f.e.m du générateur de Thevenin et Rth sa résistance interne telle que Eth=U0, Rth=Ri
Exemple:
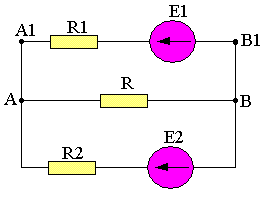
Nous nous proposons de calculer au moyen du théorème de Thevenin l'intensité traversant le dipôle (E1, R1). Il nous faut donc modifier le dipôle A1E2B1
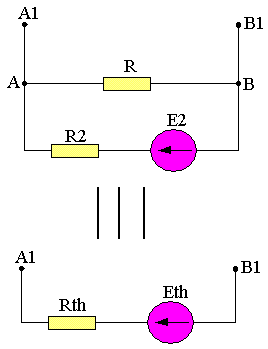
VA-VB=RI2=E2-R2I2=U0
I2=U0/R ; Eth=R.E2/(R+R2)
1/Rth=1/R+1/R2 ; Rth=R.R2/(R+R2)
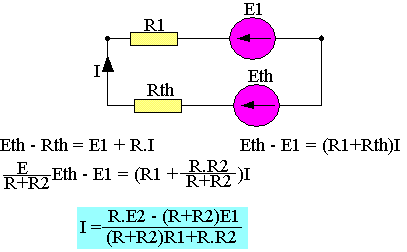
Théorème de Norton
Ce théorème nous donne une autre modélisation d'un dipôle actif. Schématisons à nouveau le dipôle actif par un générateur de Thevenin, puis établissons un court-circuit entre les bornes A et B
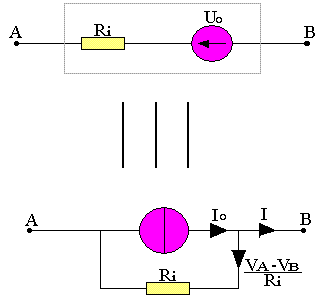
Le dipôle est traversé par un courant d'intensité I0 tel que I0=U0/Ri.
Or VA-VB=U0-RiI=U0-(VA-VB)
I=U0/Ri-(VA-VB)/Ri
I=I0-(VA-VB)/Ri
Théorème:
Un dipôle est équivalent, vu de ses deux bornes à un générateur de courant donc:
- Le courant principal I0 est le courant de court-circuit du dipôle.
- La résistance interne montée en parallèle est la résistance équivalente vue des bornes du dipôle lorsqu'on a enlevé toutes les forces électriques. Cette résistance débite un courant (VA-VB)/Ri
Application du théorème de Thevenin pour le calcul de la tension dans une branche
On considère le réseau suivant en nous proposant de calculer la différence de potentielle entre le point A et B.
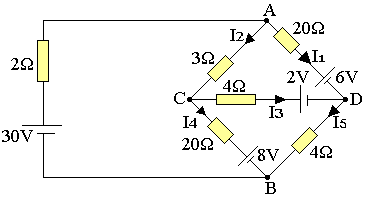
On supprime la dite branche et on écrit:
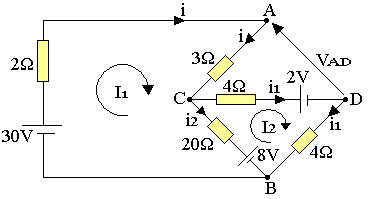
VA-VD=(VA-VC)+(VC-VB)+(VB-VD)=3i-4i1+8+20i2
Déterminons i, i1 et i2
(1): -30+2I1+3I1+20(I1-I2)+8=0 ↔ 25I1-20I2=22
(2): 4I2 +2+4I2-8+20(I2-I1)=0 ↔ -20I1+28I2=6
I1=2,45A ; I2=1,96A
i=I1=2,45A
i1=I2=1,96A
i2=i-i1=2,45-1,96=0,48A
VA-VD=3x2,45-4x1,96+20x0,48+8
VA-VB=17,11V
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale