Méthode des courants des mailles
Principe
Il ne s'agit pas d'une nouvelle méthode mais d'un moyen systématique de contourner certaines difficultés rencontrées dans la méthode de Kirchhoff. Précisons en particulier que ce moyen rend de précieux services lorsque le réseau présente un grand nombre de maille. La méthode réside dans un chargement de variable.
- On intègre que les petites mailles indépendantes sont parcourues toutes dans le même sens par les courants noté j1, j2, ..., jn
- On écrit les équations de Kirchhoff relatives aux mailles.
- On calcule les courants fictifs des mailles indépendantes et on déduit les courants réels de branche
Exemple
On considère le circuit suivant dont on se propos de calculer les intensités dans les différentes branches par la méthode des mailles fictives.
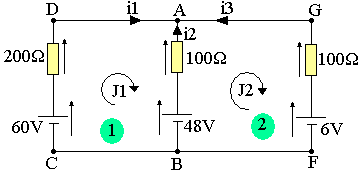
- Une branche telle que CD appartient uniquement à la maille ABCDA donc i1=J1 ; i3=J2
- Une branche telle que AB appartient aux mailles ABCDA et ABFGA, alors vue de (1) et J2-J1, vue de (2)
- maille (1)
-200J1 - 100(J1-J2) - 48 + 60 = 0
-200J1 - 100J1 + 100J2 = -12
maille (2)
100J2 - 6 + 48 + 100(J2-J1) = 0
J1=0,132A ; J2=0,276A
i1 = J1 = 0,132A
i3 = -J2 = -0,276A
i2 = i1 + i3 = 0,144A
On considère le circuit suivant
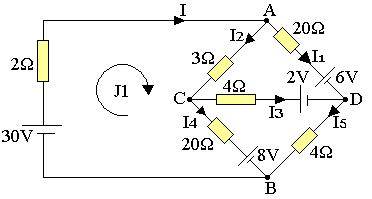
Loi des noeuds:
noeud A: I=I1+I2
noeud B: I=I4+I5
noeud C: I2=I4+I3
noeud D: I5=I1+I3
Loi des mailles
maille (1):
-30 + 2J1 + 3(J1-J2) + 20(J1-J3) + 8 = 0
25J1 - 3J2 - 20J3 = 22
maille (2):
20J2 + 6 - 2 + 4(J2-J3 + 3(J2-J1) = 0
-3J1 + 27J2 - 4J3 = -4
maille (3):
4J3 - 8 + 20(J3-J1) + 4(J3-J2) + 2 =0
-20J1 - 4J2 + 28J3 = 6
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale