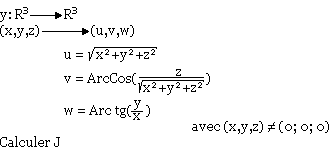Rappel sur l'espace R³

On confond l'espace géométrique à l'ensemble R³ des triplets (x, y, z) de réels.
En effet munit l'espace d'un repère orthonormé direct (o, i, j, k). Chaque point M(x, y, z) est tel que

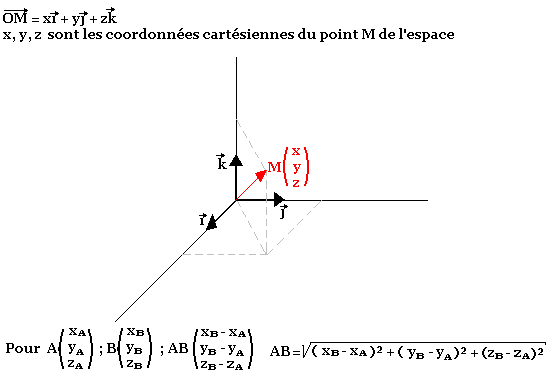
Soit un point M qui fait un déplacement élémentaire et devient M'.

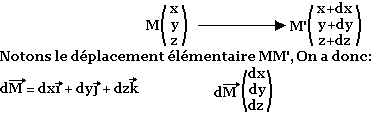
Produit scalaire

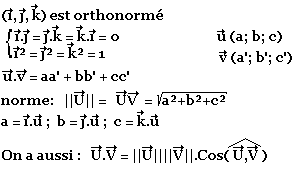
Produit vectoriel

Soient U et V deux vecteurs de l'espace, le produit vectoriel est tel que:

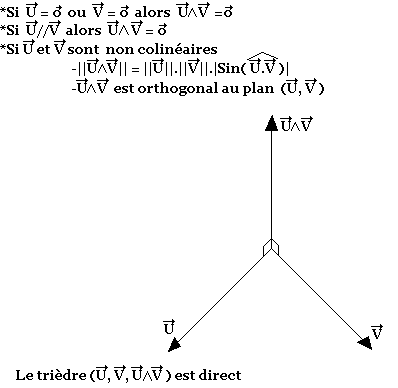
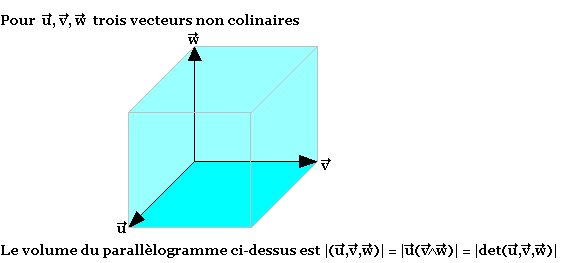
Volume:

---

Fonctions à plusieurs variables

Généralités

Il s'agit de fonctions de Rⁿ→R avec n appartenant à N et n supérieur ou égale à 2.
(x₁, x₂,...x_n)→ƒ(x₁, x₂,...,x_n)
On parle encore de champ scalaire sur Rⁿ.

Exemple 1:

f: R²→R
f(x,y) = x²e^y champ scalaire défini sur le plan R²

Exemple 2:

Un émetteur d'onde placé au point O produit une onde donc l'effet est mesurable en chaque point M(x,y,z) de l'espace à la date t par la fonction

On a une fonction à 4 variables:
µ = µ(M,t) ; M(x,y,z)
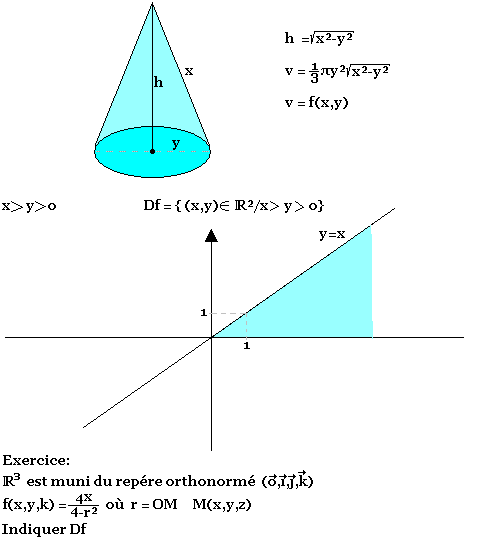
Considérons un cône de directrice x et de rayon de base y. Exprimons v volume du cône en fonction de x et y préciser l'ensemble de définition de v.

Surface de niveau

Activité:

f: IR³ → IR ; ƒ(x,y,z) = 2x+y-z
Pour toute constante k l'équation cartésienne d'un plan de l'espace. Ce plan est une surface de niveau k associée à la fonction f. En général, une surface k (k appartenant à K) est une surface d'équation ƒ(x,y,z)=k.

Exemple:

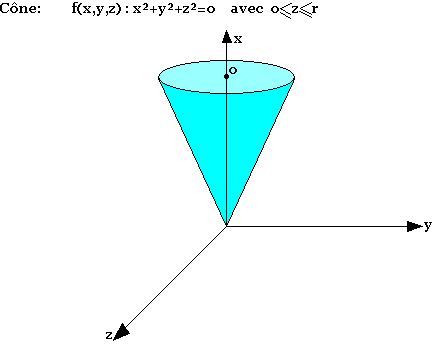
ƒ(x, y, z) = x²+y²+z² = 0 ; k=0 ; r>0
On a la sphère S[o(0;0;0), rayon r]

Courbe de niveau

ƒ: IR² → IR
Une courbe de niveau k associée à f et d'équation f(x,y)=k

Exemple:

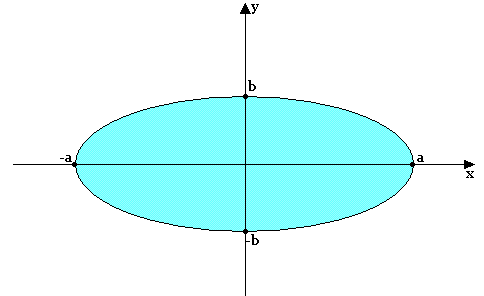
ƒ(x,y)= x²/a² + y²/b²
ƒ(x,y) = 1 ↔ x² /a² + y²/b² = 1 ; a>0 ; b>0
C'est un ellipse.

Exercice:

µ(x,y) → ArcSin(y/x)
Trouvez µ(1,-2).
Déterminez D_µ l'ensemble de définition de µ.

Continuité

M(x₀, y₀, z₀) est un point de l'ensemble de f, f est en

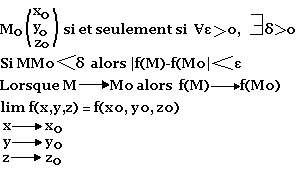
Topologie R³

Tout polynôme à plusieurs variables est continu sur son ensemble de définition.

Exemple:

P=xy³z+4x²yz²3

Toute fraction rationnelle est continue. La composée de fonction continue est continue.

Proposition:

Si ƒ est continuée sur le pavé r = [a,b]*[c,d]*[e,k] alors f est bornée sur r et atteint ses bornes:

 

---

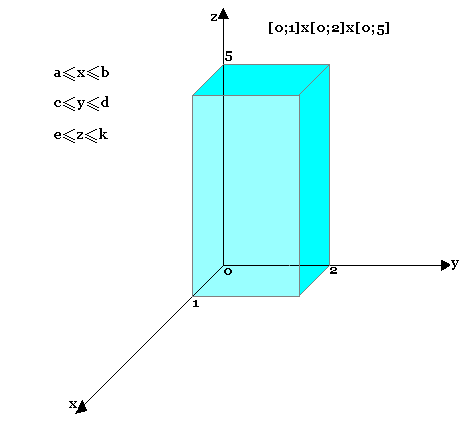
Dérivées partielles

Considérons un champ scalaire ou une fonction à 3 variables coordonnées d'un point de l'espace.
µ: M(x, y, z) → µ(M) = µ(x, y, z)
En fixant 2 variables, par exemple:
y = y₀ = constante
z = z₀ = constante
On obtient une fonction à une variable x. Si cette fonction à une variable est dérivable alors sa dérivée est encore la dérivée partielle de µ par rapport à la variable x. On écrit :

Exercices

Exercice 1:

Trouvez V la fonction x et y telle que:

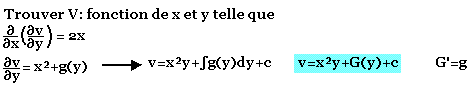
Exercice 2:

---

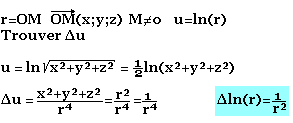
Différentielle: Opérateur gradient

Considérons une fonction définie sur une partie ouverte non vide de R³ µ:r→R
La différentielle de µ au point M₀(x₀,y₀,z₀) est la variation de µ lorsque M₀ passe de M₀ avec:

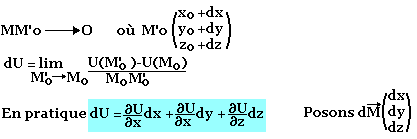
Opérateur Nabla

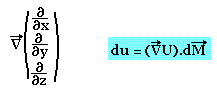
Gradient:

Le gradient de U est le champ de vecteur

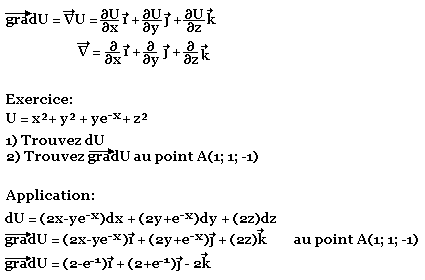
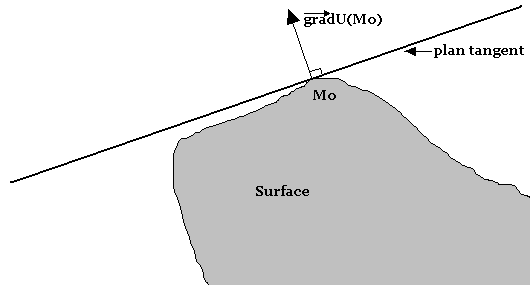
Plan tangent à une surface

Considérons la surface d'équation U(x, y, z)=c où c=constante.
Soit M₀(x₀, y₀, z₀) un point de cette surface. Le plan tangent à la surface ci-dessus au point M₀ est le plan passant par M₀ du vecteur normal.

Dérivée dans une direction

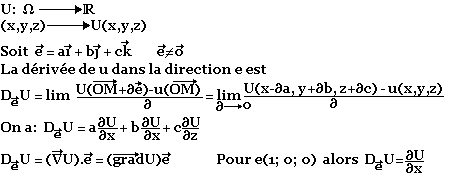
Propriétés des différentielles

u et v sont deux fonctions scalaires:

 

---

Différentielle totale

Forme différentielle: Cas de deux variables x et y

Il s'agit de la forme W=Pdx+Qdy où P et Q sont des fonctions de x et y.

Exemple:

W = 2x²dx + 4ln(y)dy

Forme différentielle: cas de trois variables x, y, z

On a ici la forme différentielle W=Pdx+Qdy+Rdz où P, Q, R sont des fonctions de x, y, z.
Une forme différentielle est dite exacte ou totale lorsqu'elle représente la différentielle d'une fonction scalaire.
W est exacte lorsqu'il existe une fonction scalaire f telle que df=W
Par exemple W=Pdx+Qdy+Rdz

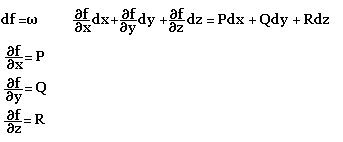
Proposition:

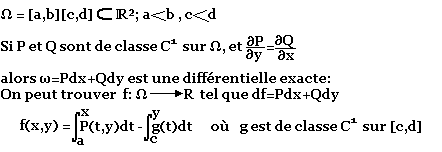
f est un ensemble de fonction tel que dƒ=W

Exemple d'application:

 

---

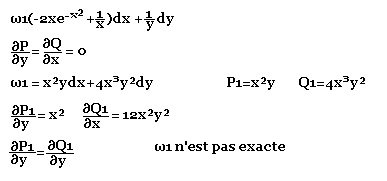
Formules d'analyse vectorielle

Un champ de vecteur est une fonction qui à chaque point M(x, y, z) associe un vecteur de l'espace.

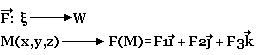
Où F₁, F₂, F₃ sont des fonctions de x, y, z.

Exemples:

Champ magnétique dans la région r de E=R³

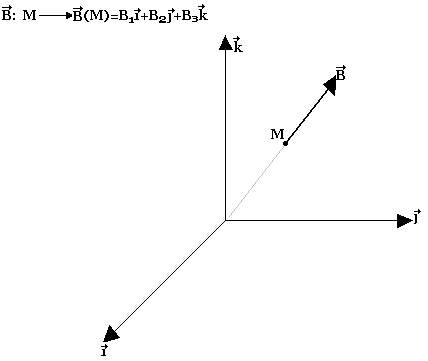
Divergence

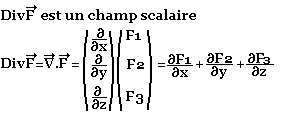
Rotationnel

Laplacien d'un champ de vecteur

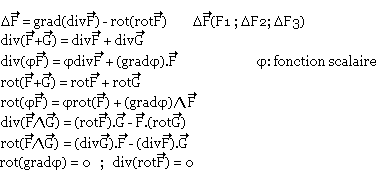
Thème:

Soit F un champ de vecteur, on dit que F dérive d'un potentiel scalaire f lorsque Rot(F)=0.

 

---

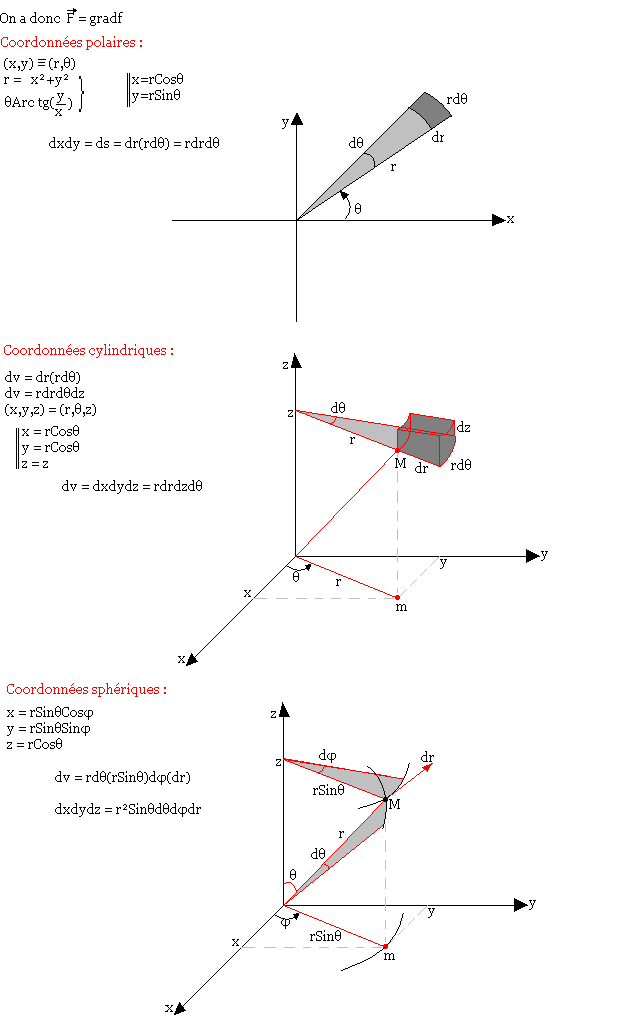
Transformation ponctuelle

Dans le plan

Où u et v sont fonction de x et y.
La matrice Jacobienne de f est:

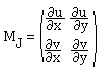
Le Jacobien de la transformation est J=det(M_J)
On a donc dxdy=Jdudv

Exemple:

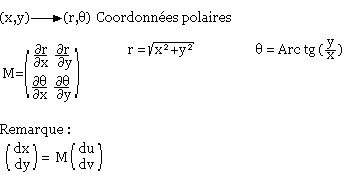
Dans l'espace (dim 3)

Exercice:

f(x, y, z) = (3x²+y, x-y²+z, 3z²)

Trouvez l'ensemble S des points M tels que le Jacobien de f en M soit non nul.