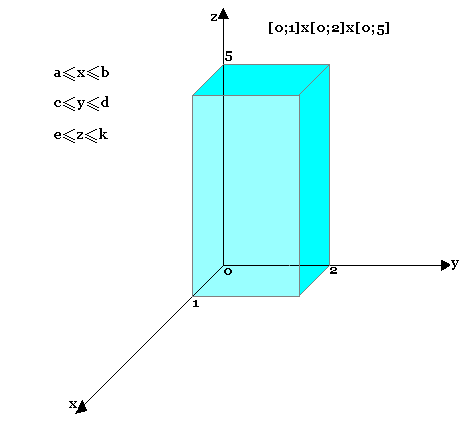
---

Fonctions à plusieurs variables

Généralités

Il s'agit de fonctions de Rⁿ→R avec n appartenant à N et n supérieur ou égale à 2.
(x₁, x₂,...x_n)→ƒ(x₁, x₂,...,x_n)
On parle encore de champ scalaire sur Rⁿ.

Exemple 1:

f: R²→R
f(x,y) = x²e^y champ scalaire défini sur le plan R²

Exemple 2:

Un émetteur d'onde placé au point O produit une onde donc l'effet est mesurable en chaque point M(x,y,z) de l'espace à la date t par la fonction

On a une fonction à 4 variables:
µ = µ(M,t) ; M(x,y,z)
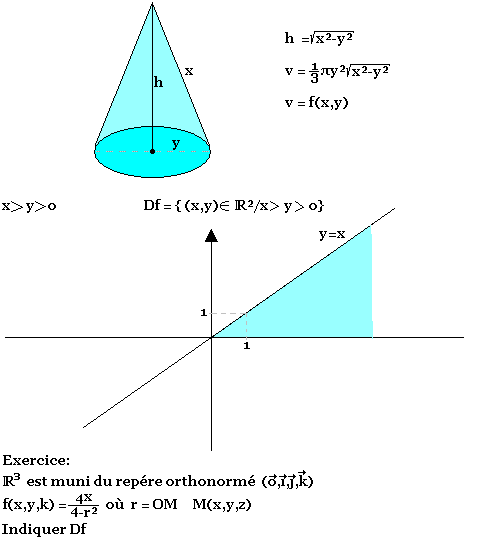
Considérons un cône de directrice x et de rayon de base y. Exprimons v volume du cône en fonction de x et y préciser l'ensemble de définition de v.

Surface de niveau

Activité:

f: IR³ → IR ; ƒ(x,y,z) = 2x+y-z
Pour toute constante k l'équation cartésienne d'un plan de l'espace. Ce plan est une surface de niveau k associée à la fonction f. En général, une surface k (k appartenant à K) est une surface d'équation ƒ(x,y,z)=k.

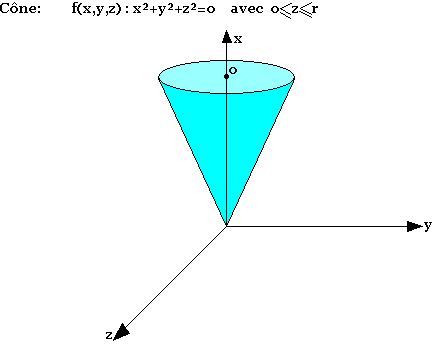
Exemple:

ƒ(x, y, z) = x²+y²+z² = 0 ; k=0 ; r>0
On a la sphère S[o(0;0;0), rayon r]

Courbe de niveau

ƒ: IR² → IR
Une courbe de niveau k associée à f et d'équation f(x,y)=k

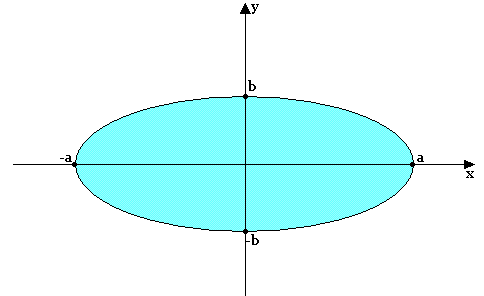
Exemple:

ƒ(x,y)= x²/a² + y²/b²
ƒ(x,y) = 1 ↔ x² /a² + y²/b² = 1 ; a>0 ; b>0
C'est un ellipse.

Exercice:

µ(x,y) → ArcSin(y/x)
Trouvez µ(1,-2).
Déterminez D_µ l'ensemble de définition de µ.

Continuité

M(x₀, y₀, z₀) est un point de l'ensemble de f, f est en

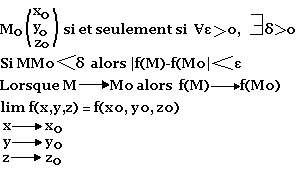
Topologie R³

Tout polynôme à plusieurs variables est continu sur son ensemble de définition.

Exemple:

P=xy³z+4x²yz²3

Toute fraction rationnelle est continue. La composée de fonction continue est continue.

Proposition:

Si ƒ est continuée sur le pavé r = [a,b]*[c,d]*[e,k] alors f est bornée sur r et atteint ses bornes: