Cas discret
On appelle variable aléatoire une grandeur qui peut prendre diverses valeurs selon les résultats d'une épreuve. Pour chaque résultat élémentaire, sa valeur étant unique. Une variable aléatoire est dite discrète si elle ne peut prendre qu'un nombre de valeur.
Fonction ou loi de répartition
On appelle fonction ou loi de répartition d'une variable aléatoire discrète toutes les valeurs possibles de ces variables et leur probabilité : pi
Exemple de loi de répartition:
|
Variables |
X |
x1 |
x2 |
... |
xx |
... |
xN |
|
Probabilité en fréquence |
P(x) |
P1 |
P2 |
... |
Pi |
... |
PN |
Exercice:
Dans une loterie de 10000 tickets, il y'a un lot de 10€, 10 lots de 1€ et 100 lots de 0,3€.
Trouvez la loi de répartition du gain aléatoire X pour le possesseur d'un seul ticket: faire le tableau.
Résolution:
|
X |
0€ |
0,3€ |
1€ |
10€ |
|
P |
0,98 |
0,01 |
0,001 |
0,0001 |
Espérance mathématique variante et écart type
Définitions
Soit une épreuve r ayant une fonction de répartition (r, X) ou X est la variable aléatoire associée à la fonction.
|
Xi |
1 |
2 |
3 |
... |
n |
|
P(x = xi) |
P1 |
P2 |
P3 |
... |
Pn |
On définit les temps suivants:
- Espérance mathématique ou moyenne statistique liée à Xi notée E(X) ou (X-). On a:
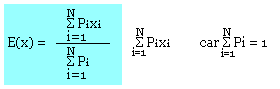
- Variance ou dispersion statique notée V(x):
![]()
- Ecart type ou dérivation standard ou écart quadratique moyen:
![]()
Autres formules
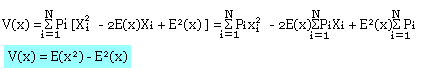
Application à un processus de Bernoulli
Soit un processus de Bernoulli à N répétition et à probabilité de succès égal à P.
|
Xi |
0 |
1 |
2 |
... |
N |
|
P(X=Xi) |
C0NqN |
C1NqN-1p |
C2NqN-2p2 |
... |
CNNpN |
On montre que pour ce processus:
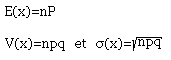
Théorème d Laplace local
![]()
Théorème de Laplace intégral
Proposons-nous de calculer la probabilité ßN[m1<m<m2;P] pour que en N épreuve de Bernoulli N tend vers l'infini, le nombre de répétition d'un événement A de probabilité P soit compris entre m1 et m2 alors
ßN[m1<m<m2;P] = PN[m1<m<m2] = PN[tm1<t<tm2 = Ø0(tm2)-Ø0(tm1)
(Valeur de Ø0 donnée en tables)
Exercices
Exercice 1:
La probabilité d'atteindre le but en tirant un seul coup de canon est P=0,1.
- Quelle est la probabilité pour que le but soit atteint au 30 fois en tirant 150 coups de canon.
- On suppose de P=0,2, on veut que m>20, quel est la probabilité pour que le but soit atteint au plus 20 fois ?
Exercice 2:
Trouvez dans les conditions du processus de Bernoulli, la probabilité pour que l'écart entre la fréquence f=m/n d'un événement A et sa probabilité P(A)=P ne soit pas en valeur absolue supérieure à 0,03.
Résolution de l'exercice 1:
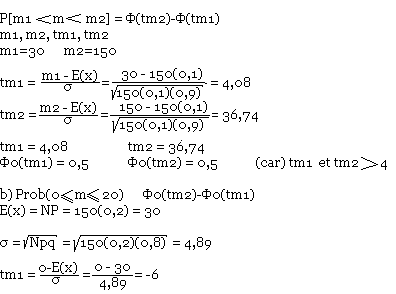
tm2 = (20-30)/4,89 = -2,06
Ø(tm1) = Ø(-6) = -Ø(6) = -0,5
Ø(tm2) = Ø(-2,04) = -Ø(2,04) = -0,48
Ø0(tm2)-Ø0(tm1) = -0,48 - (-0,5) = 0,02 = 2%
f(X) = f(X0) + (X-X0)/h
Fonction de probabilité
Densité de probabilité
Soit X une variable aléatoire associée à une loi de répartition {x1;P1}. La probabilité P(a<X<b) pour que la valeur prise par x appartenant à ]a; b[ est donnée par la formule:
![]()
Où f(x) est la densité de propagation associée à la loi (xi; Pi).
Probabilités
Si f(x) est la densité de probabilité associée à une valeur aléatoire x alors elle vérifie:
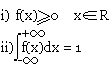
Espérance mathématique, variance
f(x) est une densité de probabilité associée à x alors
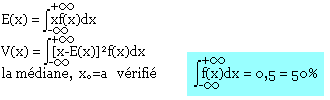
Fonction de répartition
On appelle fonction de répartition associée à la densité de probabilité f(x), la fonction F:

Exercice:
On donne la fonction f définit par:
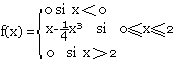
- Montrer que f est une densité de probabilité d'une variable.
- Trouver E(x) et V(x) liée à f(x).
Correction:
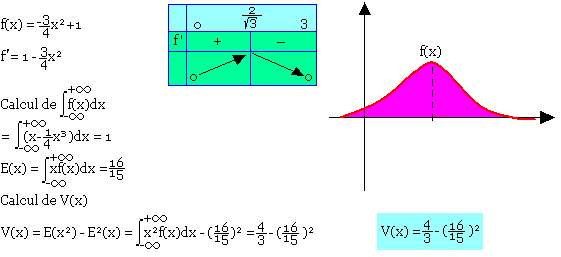
Fonction de répartition normale ou loi normale
Définition
On appelle loi de répartition normale, la loi notée:
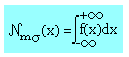
Où fN(x) est la densité de probabilité normale donnée par:
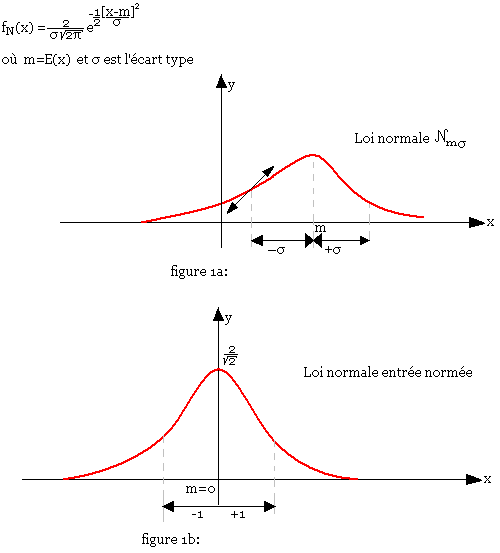
Conséquences, application
Si une variable aléatoire X suit une loi normale, alors:
![]()
Avec E(x) = m
Exercice:
Une variable aléatoire X d'espérance mathématique E(x)=1,6 et d'écart type (normé) égale à 1, est régie par la loi normale.
- Calculer la probabilité qu'a la suite d'une épreuve.
- x appartenant à ]1; 2[
- x appartenant à ]1; 3[
- Calculer la probabilité qu’à la suite de 4 épreuves, on obtient:
- au moins une fois x appartenant à [1; 2]
- exactement deux fois x appartenant à [1; 3]
Solution:
- P(1<x<2) = Ø0(2-1,6)/1 - Ø0(1-1,6)/1
= Ø0(0,4) - Ø0(-0,6) = Ø0(0,4) + Ø0(0,6) car Ø0 impaire
= 0,1554 + 0,2257
P = 0,3811 - On veut au moins un succès en 4 épreuves (E)
Contraposé: aucun succès en 4 épreuves (E)
P(E)=1-P(E) or P(E)=q4=(1-P)4
P(E)=1-P(E) = 1-[1-P]4 = 1-[1-0,38]4
Loi des grands nombres
Théorème de Bierayme-Chebitcher
Soit une variable aléatoire XN qui dépend du nombre d'épreuves N. L'espérance mathématique E(x), la variance V(x) et un nombre aussi petit que possible.
On montre l'équivalent des 2 formules suivantes:
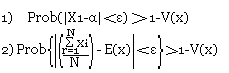
Théorème de Bernoulli
Soit N épreuve de Bernoulli pour lesquelles un événement A est obtenu µ fois avec une probabilité (succès) P.
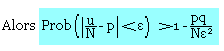
Exercice
On jette un dé 300 fois. Majorer la probabilité que la fréquence d'arrivée du côté "6" s'écarte de moins de 0,05% de la probabilité d'arrivée du côté "6".
