Fonction de répartition normale ou loi normale
Définition
On appelle loi de répartition normale, la loi notée:
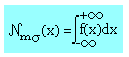
Où fN(x) est la densité de probabilité normale donnée par:
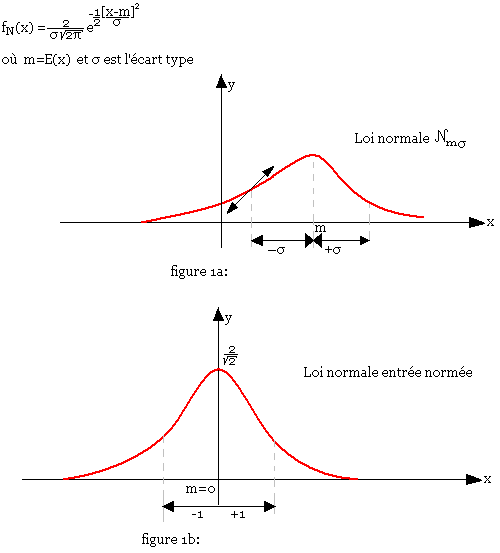
Conséquences, application
Si une variable aléatoire X suit une loi normale, alors:
Avec E(x) = m
Exercice:
Une variable aléatoire X d'espérance mathématique E(x)=1,6 et d'écart type (normé) égale à 1, est régie par la loi normale.
- Calculer la probabilité qu'a la suite d'une épreuve.
- x appartenant à ]1; 2[
- x appartenant à ]1; 3[
- Calculer la probabilité qu’à la suite de 4 épreuves, on obtient:
- au moins une fois x appartenant à [1; 2]
- exactement deux fois x appartenant à [1; 3]
Solution:
- P(1<x<2) = Ø0(2-1,6)/1 - Ø0(1-1,6)/1
= Ø0(0,4) - Ø0(-0,6) = Ø0(0,4) + Ø0(0,6) car Ø0 impaire
= 0,1554 + 0,2257
P = 0,3811 - On veut au moins un succès en 4 épreuves (E)
Contraposé: aucun succès en 4 épreuves (E)
P(E)=1-P(E) or P(E)=q4=(1-P)4
P(E)=1-P(E) = 1-[1-P]4 = 1-[1-0,38]4
Loi des grands nombres
Théorème de Bierayme-Chebitcher
Soit une variable aléatoire XN qui dépend du nombre d'épreuves N. L'espérance mathématique E(x), la variance V(x) et un nombre aussi petit que possible.
On montre l'équivalent des 2 formules suivantes:
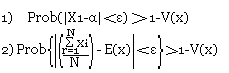
Théorème de Bernoulli
Soit N épreuve de Bernoulli pour lesquelles un événement A est obtenu µ fois avec une probabilité (succès) P.
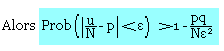
Exercice
On jette un dé 300 fois. Majorer la probabilité que la fréquence d'arrivée du côté "6" s'écarte de moins de 0,05% de la probabilité d'arrivée du côté "6".
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale